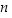pätee:
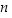pätee: Tehdään todistus matemaattisella induktiolla, ks. kurssikirjan s. 15, Lause 1.2.
a) Väite: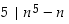 
eli väitteenä 
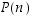on, että 
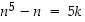jollakin 
.
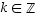1° Kun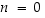 
,
väite 
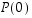pätee, sillä 
,
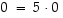missä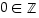 
.
2° Induktio-oletus: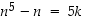 
jollakin 
.
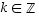3° Induktioväite: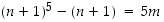 
jollakin 
.
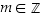Huomaa, että tässä luvun
m
ei tarvitse olla sama kuin luvun
k.
4° Induktiotodistus: Seuraavassa väitteen lauseketta sievennetään ensin sopivaan muotoon (Pascalin kolmiosta on apua binomin viidennen potenssin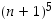 
avaamisessa), sitten neljännelle riville siirryttäessä hyödynnetään induktio-oletusta ja tämän jälkeen taas sievennetään:
Koska toiseksi viimeisen rivin lauseke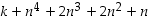 
on kokonaislukujen tulojen summana kokonaisluku, voidaan sitä merkitä muuttujalla 
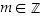ja näin ollen 
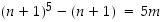ja siis 
.
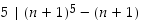Induktiotodistus saatiin valmiiksi ja siten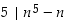 
.
b) Väite: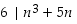 
eli väite 
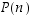on, että 
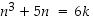jollakin 
.
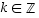1° Kun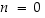 
,
väite 
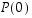pätee, sillä 
,
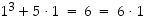missä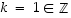 
.
2° Induktio-oletus: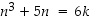 
jollekin 
.
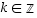3° Induktioväite: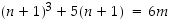 
jollekin 
.
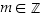(Huom! Ei tarvitse taaskaan olla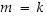 
)
4° Induktiotodistus: Käyttämällä induktio-oletusta kolmannelle riville siirryttäessä, päästään lopulta haluttuun lopputulokseen:
Riittää osoittaa, että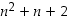 
on parillinen, sillä jälkimmäinen summattava sisältää silloin tekijöinään ainakin luvut 3 ja 2 ja on näin ollen jaollinen luvulla 6. Tällöin koko lauseke on jaollinen kuutosella, sillä kaikki summattavat ovat kuutosella jaollisia.
Osoitetaan siis, että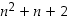 
on parillinen. Muokkaamalla lauseketta saadaan se muotoon
Koska
n
ja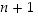 
ovat peräkkäisiä kokonaislukuja, on jompi kumpi niistä välttämättä parillinen. Luku 
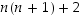eli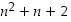 
on siis parillinen, mikä todistaa väitteen.
,
.
.