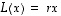 on 'tarpeeksi' ratkaisuja:
on 'tarpeeksi' ratkaisuja:
Jos lineaarikuvaukseen liittyvä matriisi on symmetrinen eli se yhtyy transpoosiinsa, voidaan osoittaa, että ominaisarvoyhtälöllä 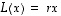 on 'tarpeeksi' ratkaisuja:
on 'tarpeeksi' ratkaisuja:
Jos lineaarikuvaukseen 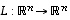 liittyvä matriisi
liittyvä matriisi 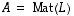 on symmetrinen, niin
on symmetrinen, niin
(a) eri ominaisarvoihin liittyvät ominaisvektorit ovat kohtisuorassa toisiaan vastaan ja
(b) sen ominaisvektoreista voidaan muodostaa avaruuden 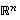 ortonormaali kanta.
ortonormaali kanta.
Todistus.
(a) Olkoot 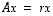 ja
ja 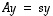 ,
missä
,
missä 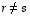 .
Silloin
.
Silloin
(b) Tämän spektraalilauseen nimellä tunnetun tuloksen todistaminen vaatisi jonkun verran ponnisteluja ja mielellään vielä kompleksilukukertoimisten vektoriavaruuksien teoriaa avukseen. Siksi se sivuutetaan tässä ja viitataan taas vain Kahanpään ja Hannukaisen luentomonisteeseen (pykälät 6.7 ja 7.6).
Edellisen esimerkin 11.4 matriisi
on symmetrinen, ts. 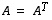 .
Valitaan mainitun esimerkin tulosten mukaisesti vektori
.
Valitaan mainitun esimerkin tulosten mukaisesti vektori 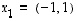 ominaisarvoon
ominaisarvoon 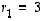 ja vektori
ja vektori 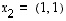 ominaisarvoon
ominaisarvoon 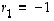 liittyväksi ominaisvektoriksi. Silloin havaitaan, että
liittyväksi ominaisvektoriksi. Silloin havaitaan, että 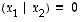 ,
joten ne ovat todellakin kohtisuorassa toisiaan vastaan.
,
joten ne ovat todellakin kohtisuorassa toisiaan vastaan.
Normitetaan ne vielä ykkösen pituisiksi, ts. valitaan
jolloin saadut ominaisvektorit 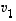 ja
ja 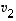 muodostavat tason ortonormaalin kannan. Piirrä tilanteesta itsellesi havainnollistava kuva!
muodostavat tason ortonormaalin kannan. Piirrä tilanteesta itsellesi havainnollistava kuva!
Tarkastellaan symmetristä matriisia
Määrätään ensin sen karakteristinen yhtälö:
Tässä ehdosta 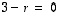 saadaan ratkaisu
saadaan ratkaisu 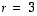 ja toisaalta yhtälön
ja toisaalta yhtälön 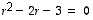 juuret ovat
juuret ovat 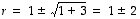 .
Siten näistä karakteristisen yhtälön kaikista ratkaisuista saadaan koottua ominaisarvoiksi
.
Siten näistä karakteristisen yhtälön kaikista ratkaisuista saadaan koottua ominaisarvoiksi 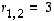 ja
ja 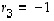 .
.
Määrätään seuraavaksi ominaisvektorit. Tehdään se ensin ominaisarvolle 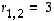 ratkaisemalla ominaisarvoyhtälö
ratkaisemalla ominaisarvoyhtälö 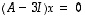 Gaussin ja Jordanin menetelmällä:
Gaussin ja Jordanin menetelmällä:
Valitsemalla tässä vuoronperään parametrit 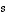 ja
ja 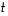 nolliksi ja ykkösiksi saadaan kaksi kohtisuoraa ominaisvektoria (kohtisuoruuden saavuttaminen oli olennaista). Normitetaan ne samalla ykkösen pituisiksi eli valitaan siis ensimmäiseen ominaisarvoon liittyviksi ominaisvektoreiksi vektorit
nolliksi ja ykkösiksi saadaan kaksi kohtisuoraa ominaisvektoria (kohtisuoruuden saavuttaminen oli olennaista). Normitetaan ne samalla ykkösen pituisiksi eli valitaan siis ensimmäiseen ominaisarvoon liittyviksi ominaisvektoreiksi vektorit
Määrätään toiseksi ominaisvektorit ominaisarvolle 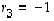 :
:
Valitaan tästä ratkaisusta ykkösen pituinen ominaisvektori
Saadut ominaisvektorit 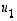 ,
,
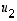 ja
ja 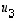 muodostavat nyt todella ortonormaalin kannan.
muodostavat nyt todella ortonormaalin kannan.
Paitsi se, että symmetrisen matriisin ominaisvektoreista voidaan muodostaa ortonormaali kanta, vielä tärkeämpää on, että lineaarikuvausta vastaa siinä kannassa hyvin yksinkertainen matriisi.
Oletetaan, että lineaarikuvaukseen 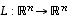 liittyvä matriisi
liittyvä matriisi 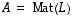 on symmetrinen ja olkoon
on symmetrinen ja olkoon 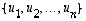 sen ominaisvektoreista muodostettu ortonormaali kanta, jolloin siis
sen ominaisvektoreista muodostettu ortonormaali kanta, jolloin siis 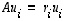 vastaaville ominaisarvoille
vastaaville ominaisarvoille 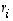 .
Silloin kuvausta
.
Silloin kuvausta 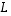 vastaa kannassa
vastaa kannassa 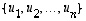 diagonaalimatriisi
diagonaalimatriisi
Todistus.
Muodostetaan matriisi 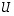 niin, että ominaisvektorit
niin, että ominaisvektorit 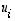 sijoitetaan sen sarakkeiksi. Se on silloin lauseen 8.17 mukaan ortogonaalinen matriisi ja siten
sijoitetaan sen sarakkeiksi. Se on silloin lauseen 8.17 mukaan ortogonaalinen matriisi ja siten 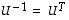 .
Kannanvaihtolauseen 9.4 mukaan taas matriisi
.
Kannanvaihtolauseen 9.4 mukaan taas matriisi
vastaa lineaarikuvausta 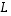 kannassa
kannassa 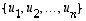 .
Tämän matriisin ensimmäinen sarake on vektori
.
Tämän matriisin ensimmäinen sarake on vektori
Vastaavasti laskettuna muille sarakkeille saadaan, että 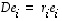 ,
mikä todistaakin väitteen. Sama tulos nähdään toki suoraankin siitä, että yhtälöiden
,
mikä todistaakin väitteen. Sama tulos nähdään toki suoraankin siitä, että yhtälöiden 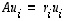 mukaan myös yhtälöt
mukaan myös yhtälöt 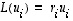 pätevät.
pätevät.
Jatketaan edellistä esimerkkiä 11.7. Siinä saaduista matriisin 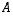 ominaisvektoreista
ominaisvektoreista 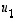 ,
,
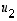 ja
ja 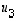 muodostettu kannanvaihtomatriisi on nyt
muodostettu kannanvaihtomatriisi on nyt
ja teorian mukaisesti tiedetään siis laskemattakin (minkä voi tietenkin tarkistaa), että
Toisin sanoen, matriisia 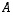 vastaavalle lineaarikuvaukselle
vastaavalle lineaarikuvaukselle 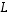 ,
,
Huomaa esimerkin mukaisissa tilanteissa, että ominaisvektorit 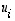 ja niitä vastaavat ominaisarvot
ja niitä vastaavat ominaisarvot 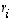 on sijoitettava matriisien
on sijoitettava matriisien 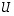 ja
ja 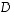 sarakkeille täsmälleen samassa järjestyksessä, jotta matriisitulo
sarakkeille täsmälleen samassa järjestyksessä, jotta matriisitulo 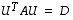 toteutuu.
toteutuu.
Havainnollistus: Lineaarikuvauksen ominaisarvot ja ominaisvektorit