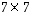Mathematica-esimerkki

Seuraavassa on esimerkki erään 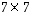-matriisin ominaisarvojen laskemisesta ja diagonalisoinnista Mathematica?-ohjelmalla. (Suorituskomentojen tarkoituksen voi arvata niiden nimistä ja muodoista.)

Matriisin määrittely

f[i_,j_] := If[i==j, 1, 2]; n = 7; A = Array[f, {n,n}]; MatrixForm[A]

1 2 2 2 2 2 2

2 1 2 2 2 2 2

2 2 1 2 2 2 2

2 2 2 1 2 2 2

2 2 2 2 1 2 2

2 2 2 2 2 1 2

2 2 2 2 2 2 1

Karakteristisen polynomin laskeminen

id = IdentityMatrix[n]; MatrixForm[A - x*id]

1 - x 2 2 2 2 2 2

2 1 - x 2 2 2 2 2

2 2 1 - x 2 2 2 2

2 2 2 1 - x 2 2 2

2 2 2 2 1 - x 2 2

2 2 2 2 2 1 - x 2

2 2 2 2 2 2 1 - x

p = Det[A - x*id]

2 3 4 5 6 7

13 + 77 x + 189 x + 245 x + 175 x + 63 x + 7 x - x

Factor[p]

6

(13 - x) (1 + x)

Ominaisarvojen ratkaiseminen

s = Solve[p==0, x]

{{x -> -1}, {x -> -1}, {x -> -1}, {x -> -1}, {x -> -1},

{x -> -1}, {x -> 13}}

r = x/.s

{-1, -1, -1, -1, -1, -1, 13}

Ominaisvektorien laskeminen

V1 = NullSpace[A - r[[1]]*id]

{{-1, 0, 0, 0, 0, 0, 1}, {-1, 0, 0, 0, 0, 1, 0},

{-1, 0, 0, 0, 1, 0, 0}, {-1, 0, 0, 1, 0, 0, 0},

{-1, 0, 1, 0, 0, 0, 0}, {-1, 1, 0, 0, 0, 0, 0}}

vn = NullSpace[A - r[[n]]*id]

{{1, 1, 1, 1, 1, 1, 1}}

Sama suoraan!

Eigenvalues[A]

{-1, -1, -1, -1, -1, -1, 13}

e = Eigenvectors[A]

{{-1, 0, 0, 0, 0, 0, 1}, {-1, 0, 0, 0, 0, 1, 0},

{-1, 0, 0, 0, 1, 0, 0}, {-1, 0, 0, 1, 0, 0, 0},

{-1, 0, 1, 0, 0, 0, 0}, {-1, 1, 0, 0, 0, 0, 0},

{1, 1, 1, 1, 1, 1, 1}}

Diagonalisoinnin tarkistus

U = Transpose[e]; MatrixForm[U]

-1 -1 -1 -1 -1 -1 1

0 0 0 0 0 1 1

0 0 0 0 1 0 1

0 0 0 1 0 0 1

0 0 1 0 0 0 1

0 1 0 0 0 0 1

1 0 0 0 0 0 1

MatrixForm[Inverse[U].A.U]

-1 0 0 0 0 0 0

0 -1 0 0 0 0 0

0 0 -1 0 0 0 0

0 0 0 -1 0 0 0

0 0 0 0 -1 0 0

0 0 0 0 0 -1 0

0 0 0 0 0 0 13

% == DiagonalMatrix[Eigenvalues[A]]

True