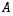 sanotaan
ortogonaaliseksi, jos se on kääntyvä ja
sanotaan
ortogonaaliseksi, jos se on kääntyvä ja 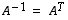 eli jos
eli jos 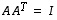 tai
tai 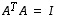 .
.
Transpoosin avulla saadaan kuvattua nopeasti eräs geometrisesti tärkeä muunnostyyppi, nimittäin sellainen, joka muuntaa ortonormaalin kannan ortonormaaliksi kannaksi.
Ensinnä nimitys. Neliömatriisia 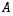 sanotaan
ortogonaaliseksi, jos se on kääntyvä ja
sanotaan
ortogonaaliseksi, jos se on kääntyvä ja 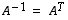 eli jos
eli jos 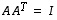 tai
tai 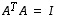 .
.
Seuraavaksi selvitetään yhteys geometriaan. Vektorin ja sarakematriisin samaistuksen jälkeen sisätulo voidaan ajatella myös matriisitulona, sillä vektoreille 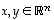 on
on
Tämän mukaisesti voidaan edelleen ajatella, että matriisitulossa 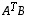 sen alkiot ovat matriisien
sen alkiot ovat matriisien 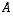 ja
ja 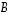 sarakevektoreiden sisätuloja. Sisätulon avulla taas saatiin laskettua vektoreiden pituudet ja niiden väliset kulmat kuten luvussa 5 selvitettiin.
sarakevektoreiden sisätuloja. Sisätulon avulla taas saatiin laskettua vektoreiden pituudet ja niiden väliset kulmat kuten luvussa 5 selvitettiin.
Kun nyt ortogonaalisuuden ehto 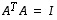 puretaan auki, se vaatii itse asiassa sen, että matriisin
puretaan auki, se vaatii itse asiassa sen, että matriisin 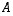 sarakevektoreiden eli sarakkeista muodostettujen avaruuden
sarakevektoreiden eli sarakkeista muodostettujen avaruuden 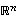 vektoreiden on sekä oltava kohtisuorassa toisiaan vastaan että ykkösen pituisia - eli lyhyemmin sanottuna niiden on muodostettava ortonormaali kanta. Tästä historiallisesti tuleekin ortogonaalisuus-nimitys, mutta on huomattava, että sarakevektoreilta vaaditaan kuitenkin enemmän kuin mitä pelkkään kohtisuoruuteen viittaava nimi antaisi olettaa. Kohtisuoruuden lisäksi niiden on oltava nimittäin yksikön pituisia.
vektoreiden on sekä oltava kohtisuorassa toisiaan vastaan että ykkösen pituisia - eli lyhyemmin sanottuna niiden on muodostettava ortonormaali kanta. Tästä historiallisesti tuleekin ortogonaalisuus-nimitys, mutta on huomattava, että sarakevektoreilta vaaditaan kuitenkin enemmän kuin mitä pelkkään kohtisuoruuteen viittaava nimi antaisi olettaa. Kohtisuoruuden lisäksi niiden on oltava nimittäin yksikön pituisia.
Seuraava tulos on edellä tullut perusteltua.
Jos lineaarikuvaus kuvaa luonnollisen kannan ortonormaaliksi kannaksi, sitä vastaa ortogonaalinen matriisi. Kääntäen, jos lineaarikuvausta vastaava matriisi on ortogonaalinen, se muuntaa luonnollisen kannan ortonormaaliksi kannaksi.
Sellainen lineaarikuvaus, joka kuvaa, kuten yllä olevassa lauseessa, luonnollisen kannan ortonormaaliksi kannaksi, on itse asiassa bijektio, joka säilyttää kaikki vektorien väliset kulmat ja niiden pituudet. Tällaista kuvausta sanotaan myös isometriseksi lineaarikuvaukseksi tai (lineaariseksi) isometriaksi.
Tason peilausta vaaka-akselin suhteen vastaa matriisi
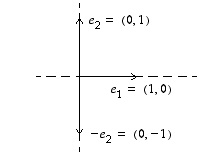
Siten 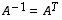 osoittaen, että matriisi
osoittaen, että matriisi 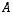 on ortogonaalinen. Tämä vastaa myös geometrista havaintoa siitä, että peilauksessa luonnollinen (ortonormaali) kanta kuvautuu ortonormaaliksi kannaksi ts. tässä muunnoksessa vektoreiden kohtisuoruudet ja niiden välisten kulmien suuruudet säilyvät.
on ortogonaalinen. Tämä vastaa myös geometrista havaintoa siitä, että peilauksessa luonnollinen (ortonormaali) kanta kuvautuu ortonormaaliksi kannaksi ts. tässä muunnoksessa vektoreiden kohtisuoruudet ja niiden välisten kulmien suuruudet säilyvät.
Tason kiertoa kulman 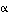 verran vastapäivään vastaa matriisi
verran vastapäivään vastaa matriisi
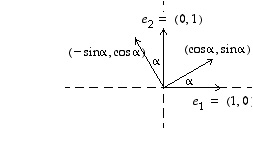
Siten 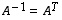 eli matriisi
eli matriisi 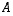 on ortogonaalinen. Nytkin tämä vastaa geometrista havaintoa siitä, että kierrossa luonnollinen kanta kuvautuu ortonormaaliksi kannaksi.
on ortogonaalinen. Nytkin tämä vastaa geometrista havaintoa siitä, että kierrossa luonnollinen kanta kuvautuu ortonormaaliksi kannaksi.