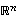
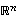
Yleinen euklidinen avaruus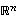 
(kun 
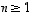) on vektoriavaruus, kun sen alkioille, 
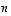-jonoille ja nyt myös vektoreiksi kutsutuille
sekä luvulle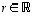 
asetetaan, että vektorien 
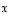ja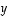 
summa on
Lauseessa 2.2 luetellut säännöt pätevät tässäkin avaruudessa. Tapauksissa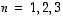 
kyseessä ovat tietenkin edellä käsitellyt suora, taso ja avaruus.
Avaruudessa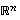 
nollavektori on 
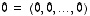ja vektorin 
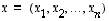vastavektori on vektori 
.
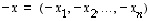Edelleen sen
luonnollisen
kannan muodostavat vektorit
Jokainen vektori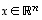 
voidaan edelleen yksikäsitteisesti esittää
lineaarikombinaationa
Kertoimia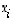 
sanotaan myös vektorin 
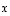koordinaateiksi. Yllä esiintyvä 'pitkä' summa voidaan
summausmerkkiä ja yleistä
summausindeksiä käyttäen kirjoittaa myös muotoon
Havainnollistus: Vektoreiden lineaarikombinaatio
Havainnollistus: Vektoreiden yhteenlasku (1)
Havainnollistus: Vektoreiden vähennyslasku
Havainnollistus: Vektoreiden yhteenlasku (2)
monikerta
.
.
.