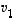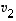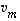,
,
..., 
virittävät avaruuden 
,
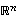jos jokainen vektori 
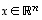voidaan lausua jonakin näiden lineaarikombinaationa
Katsotaan sitten, mitä vektoreita saadaan annettujen vektoreiden lineaarikombinaatioina. Joskus saadaan kaikki tarkasteltavan avaruuden vektorit, mutta ei tietenkään aina. Sanotaankin, että vektorit ,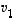
,
...,
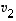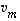virittävät avaruuden ,
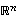jos jokainen vektori 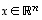voidaan lausua jonakin näiden lineaarikombinaationa
Huomaa, että lukujen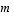 
ja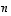 
ei tässä tarvitse olla samoja kokonaislukuja.
Virittäminen voi olla suoraan määrittelyn mukaan tehtynä työlästä tarkistaa. Kehitetäänkin tämän toteamiseksi nopeampi päättelytapa.
Merkitään avaruuden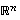 
vektoreille 
,
,
..., 
,
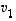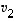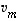että
Tämä on ns. vektoreiden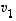 
,
,
..., 
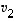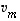virittämä
aliavaruus.
Yleensäkin
aliavaruuksilla on se karakteristinen ominaisuus, että kaikki niiden vektorien lineaarikombinaatiot ovat edelleen sen vektoreita. Ne muodostavat siten tavallaan omia vektoriavaruuksiaan. Esimerkiksi origon kautta kulkevat suorat ja tasot ovat kaikki tämän mukaisesti aliavaruuksia avaruudessa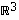 
.
Itse asiassa myöhemmin esimerkissä 6.13 todetaan, että muun tyyppisiä aliavaruuksia ei olekaan. Huomaa lisäksi, että jokainen aliavaruus sisältää aina avaruuden nollavektorin.
Tarkastellaan avaruuden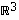 
osajoukkoa
Jos nyt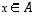 
ja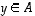 
,
saadaan summavektorin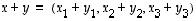 
komponenteille laskettua, että
Tämä osoittaa, että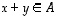 
.
Jos lisäksi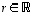 
,
saadaan vastaavasti monikertavektorille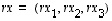 
,
että
Siten myös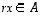 
.
Edellä olevan määrittelyn mukaan joukko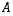 
on siten avaruuden 
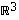aliavaruus. Määrittelyjen yhteensopivuuden vuoksi sen täytyisi olla myös esitettävissä joidenkin vektoreiden virittämänä aliavaruutena. Todennetaan vielä se.
Vektorin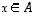 
komponenteille on voimassa ehto 
,
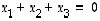joka voidaan lausua myös muodossa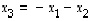 
.
Kolmas komponentti on näin ollen määrätty, jos kaksi ensimmäistä tiedetään. Tämän mukaisesti kokeillaan valita vektorit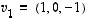 
ja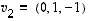 
.
Silloin jokainen vektori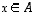 
voidaan esittää muodossa
Tämä osoittaakin, että joukko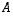 
on vektorien 
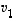ja 
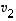virittämä aliavaruus eli 
.
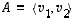Seuraavassa päämääränä on ratkaista koko avaruuden virittämiskysymys pelkästään lineaarisen riippumattomuuden ja vektoreiden lukumäärän avulla. Sitä varten tarvitaan ensin muutamia valmistavia tuloksia. Ensimmäinen näistä on ehkä teknisen tuntuinen muotoilultaan ja todistukseltaan, mutta se on tarpeellinen avaintulos myöhemmille tuloksille.
Jos vektori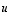 
on vektorien 
,
,
..., 
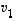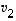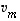lineaarikombinaatio, niin
Todistus.
Koska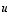 
on vektorien 
,
,
..., 
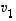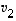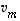lineaarikombinaatio, voidaan jokaisessa vektorien 
,
,
,
..., 
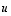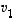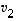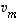lineaarikombinaatiossa vektori 
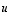korvata muiden lineaarikombinaatiolla, jolloin tuloksena on pelkästään vektorien 
,
,
..., 
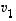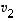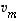lineaarikombinaatio.
Jos avaruuden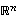 
vektorit 
,
,
..., 
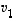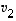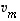ovat lineaarisesti riippumattomat ja jos vektorit 
,
,
..., 
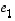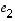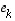virittävät avaruuden 
,
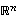on oltava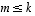 
.
Todistus.
Seuraavassa esitetään todistuksesta pääpiirteet joitakin yksityiskohtaisia laskelmia ohittaen. Koska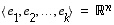 
,
vektorilla 
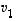on esitys
Tässä esityksessä jokin kerroin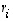 
on nollasta eroava, sillä muutoin 
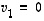vastoin vektoreiden 
,
,
..., 
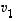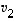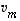lineaarista riippumattomuutta. Olkoon 
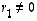(muut tapaukset voidaan indeksejä muuttamalla hoitaa vastaavasti). Yltä voidaan silloin ratkaista, että
Edellisen lauseen 4.7 mukaan on täten
Niinpä vektorilla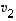 
on jokin esitys
Jos tässä oli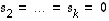si 
,
olisi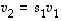 
ja siten joukko 
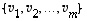olisi vastoin oletusta lineaarisesti riippuva. Jonkin näistä kertoimista on siis oltava nollasta eroava, olkoon se 
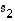(muut tapaukset voidaan hoitaa taas indeksejä muuttamalla). Samaan tapaan kuin edellä voidaan ratkaista
Tällä tavalla jatketaan, ts. jokainen vektori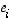 
korvataan vuorollaan vektorilla 
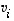ja joka vaiheessa päätellään, että näin saatu vektorijoukko virittää edelleen koko avaruuden.
Jos nyt olisi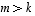 
vastoin väitettä, saataisiin tulokseksi, että
Tällöin käyttämättä jäänyt vektorikin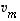 
olisi kyseisessä aliavaruudessa ts. se olisi muiden vektoreiden 
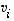lineaarikombinaatio. Tämä taas tarkoittaisi, että vektorit 
,
,
..., 
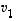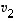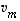olisivat lineaarisesti riippuvat - vastoin oletusta. Ei siis voi olla 
,
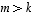vaan täytyy olla 
,
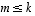kuten väitettiin.
.
.
.
.
.
.
.
.
.
.
.
