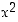 ja
ja 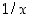 derivaatat määritelmän mukaisesti eli määräämällä erotusosamäärien raja-arvot.
derivaatat määritelmän mukaisesti eli määräämällä erotusosamäärien raja-arvot.
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
112. Muodosta funktioiden 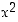 ja
ja 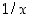 derivaatat määritelmän mukaisesti eli määräämällä erotusosamäärien raja-arvot.
derivaatat määritelmän mukaisesti eli määräämällä erotusosamäärien raja-arvot.
113. Määrää funktiolle 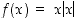 derivaatta
derivaatta 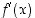 pisteissä
pisteissä 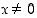 (derivoimissäännöin) ja pisteessä
(derivoimissäännöin) ja pisteessä 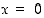 (erotusosamäärällä). Piirrä funktion ja sen derivaatan kuvaajat.
(erotusosamäärällä). Piirrä funktion ja sen derivaatan kuvaajat.
114. Todista (derivoinnin summakaava lauseesta 3.3.1), että
kun funktiot 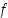 ja
ja 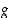 ovat derivoituvia pisteessä
ovat derivoituvia pisteessä 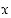 .
.
115. Millä luvun 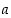 arvoilla paraabelien
arvoilla paraabelien 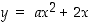 ja
ja 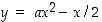 tangentit origossa ovat kohtisuorassa toisiaan vastaan?
tangentit origossa ovat kohtisuorassa toisiaan vastaan?
116. Millä luvun 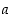 arvoilla käyrillä
arvoilla käyrillä 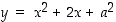 ja
ja 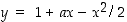 on jossakin pisteessä yhteinen vaakasuora tangentti?
on jossakin pisteessä yhteinen vaakasuora tangentti?
117. Muodosta funktion 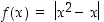 derivaatta niissä pisteissä, joissa se on mahdollista. Piirrä funktion ja sen derivaatan kuvaajat.
derivaatta niissä pisteissä, joissa se on mahdollista. Piirrä funktion ja sen derivaatan kuvaajat.
derivaatta 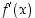 pisteissä
pisteissä 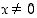 . (Vrt. tehtävä 106)
. (Vrt. tehtävä 106)
119. Laske seuraavien funktioiden derivaatat
120. Reaalifunktion 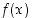 derivaatasta tiedetään, että
derivaatasta tiedetään, että 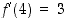 . Määrää seuraavat raja-arvot:
. Määrää seuraavat raja-arvot:
121. Määrää funktion 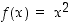 ,
missä
,
missä 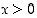 ,
käänteisfunktion derivaatta pisteessä 2 sekä eksplisiittisesti (ratkaisemalla ensin käänteisfunktio), että implisiittisesti (ratkaisematta käänteisfunktiota).
,
käänteisfunktion derivaatta pisteessä 2 sekä eksplisiittisesti (ratkaisemalla ensin käänteisfunktio), että implisiittisesti (ratkaisematta käänteisfunktiota).
122. Oletetaan tiedetyksi, että funktiolla 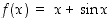 on käänteisfunktio. Määrää käänteisfunktion derivaatta pisteessä
on käänteisfunktio. Määrää käänteisfunktion derivaatta pisteessä 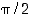 . Mikä on tangentin yhtälö silloin? Piirrä tilanteesta kuva.
. Mikä on tangentin yhtälö silloin? Piirrä tilanteesta kuva.