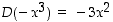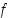 ja
ja 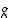 derivoituvia pisteessä
derivoituvia pisteessä 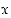 . Tällöin pätevät seuraavat:
. Tällöin pätevät seuraavat:
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Selvitetään ensin, millaisia sääntöjä voidaan löytää rationaalisten lausekkeiden derivaatoille, mikäli lausekkeen muodostavien osafunktioiden derivaatat tunnetaan. Erityisesti näitä sääntöjä voidaan sitten käyttää polynomien ja rationaalifunktioiden derivaattojen muodostamiseen.
Olkoot funktiot 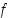 ja
ja 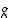 derivoituvia pisteessä
derivoituvia pisteessä 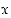 . Tällöin pätevät seuraavat:
. Tällöin pätevät seuraavat:
Todistus. Kohta (a) on suoraviivainen todistaa erotusosamäärien avulla ja sivuutetaan tässä.
(b) Muodostetaan tuloon liittyvä erotusosamäärä ja selvitetään sen raja-arvo:
Yllä raja-arvon määräämisessä on käytetty funktioiden 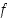 ja
ja 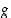 derivaatan olemassaoloa ja funktion
derivaatan olemassaoloa ja funktion 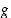 jatkuvuutta pisteessä
jatkuvuutta pisteessä 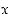 .
.
(c) Muodostetaan nyt funktioon 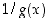 liittyvä erotusosamäärä ja selvitetään sen raja-arvo:
liittyvä erotusosamäärä ja selvitetään sen raja-arvo:
(d) Edellisten kohtien perusteella on
Esimerkin 3.2.5 mukaan 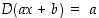 (kun
(kun 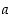 ja
ja 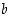 ovat vakioita). Erikoisesti vakiofunktion derivaatta on nolla. Edellä olevan tulon derivoimissäännön mukaan on edelleen
ovat vakioita). Erikoisesti vakiofunktion derivaatta on nolla. Edellä olevan tulon derivoimissäännön mukaan on edelleen
kun 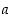 on vakio. Tämä nähdään valitsemalla mainitussa säännössä
on vakio. Tämä nähdään valitsemalla mainitussa säännössä 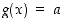 .
.
Esimerkin 3.2.3 mukaan funktion 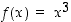 derivaatta on
derivaatta on 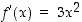 . Siten esimerkiksi
. Siten esimerkiksi 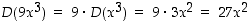 ja vastaavasti
ja vastaavasti