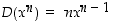 ,
kun
,
kun 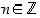 ,
,
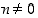 .
.
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Käyttäen edellisen lauseen sääntöjä toistuvasti saadaan näistä edelleen johdettua seuraavat potenssi-, polynomi- ja rationaalifunktioiden derivoimissäännöt.
Seuraavat derivoimissäännöt pätevät:
on kaikkialla derivoituva ja sen derivaatta on
(Tapauksessa 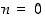 ,
eli kun
,
eli kun 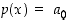 ,
on
,
on 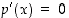 .)
.)
(c) Rationaalifunktiot ovat derivoituvia määrittelyjoukossaan ja niiden derivaatat ovat edelleen rationaalifunktioita. Derivaatta muodostetaan osamäärän derivoimissäännöllä ja polynomin derivoimissäännöin.
Todistus. (a) Olkoon ensin 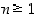 . Funktiolle
. Funktiolle 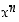 on silloin
on silloin
Tämä kohta voidaan todistaa myös induktiolla käyttäen tulon derivoimissääntöä apuna. Tehdään se myös niin. Kun 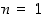 ,
pätee kaava. Kun sitten oletetaan, että
,
pätee kaava. Kun sitten oletetaan, että 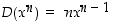 jollekin
jollekin 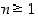 ,
niin
,
niin
Olkoon sitten 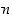 negatiivinen, jolloin
negatiivinen, jolloin 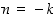 ,
missä
,
missä 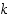 on positiivinen. Funktiolle
on positiivinen. Funktiolle 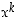 on silloin edellä todistetun mukaan
on silloin edellä todistetun mukaan 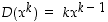 . Osamäärän derivoinnilla saadaan siten
. Osamäärän derivoinnilla saadaan siten
(b) Tulos seuraa summan derivoimissäännöstä ja edellisestä kohdasta.
(c) Edellisen kohdan mukaan polynomien derivaatat ovat polynomeja, joten osamäärän derivoimissäännön mukaan rationaalifunktioiden derivaatat ovat edelleen rationaalifunktioita.
derivaatta on kaikkialla olemassa, koska itse funktio on rationaalifunktio, joka on kaikkialla määritelty (sillä 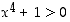 aina). Derivaatta saadaan laskettua osamäärän ja polynomin derivoimissäännöillä:
aina). Derivaatta saadaan laskettua osamäärän ja polynomin derivoimissäännöillä:
on määritelty, kun 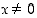 ,
ja sen derivaatta on silloin
,
ja sen derivaatta on silloin
Havainnollistus: Funktiosta jatkuva ja derivoituva 
Laskentapohja: Arvaa jatkuvuusvakiot 
Opiskeluvideo: D3: Osamäärän derivaatta 
