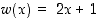 ,
kun
,
kun 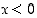 ,
jonka kuvaaja on kuvassa sininen suoran osa. Tätä funktiota pitää jatkaa sellaisella funktiolla, että yhteenliitetystä funktiosta tulee jatkuva ja derivoituva kohdassa nolla.
,
jonka kuvaaja on kuvassa sininen suoran osa. Tätä funktiota pitää jatkaa sellaisella funktiolla, että yhteenliitetystä funktiosta tulee jatkuva ja derivoituva kohdassa nolla.
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Tarkoituksena on tehdä kohdassa nolla epäjatkuvasta funktiosta jatkuva ja derivoituva erilaisissa tilanteissa. Jatkettavana funktiona on 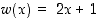 ,
kun
,
kun 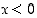 ,
jonka kuvaaja on kuvassa sininen suoran osa. Tätä funktiota pitää jatkaa sellaisella funktiolla, että yhteenliitetystä funktiosta tulee jatkuva ja derivoituva kohdassa nolla.
,
jonka kuvaaja on kuvassa sininen suoran osa. Tätä funktiota pitää jatkaa sellaisella funktiolla, että yhteenliitetystä funktiosta tulee jatkuva ja derivoituva kohdassa nolla.
Kuvan alla on kolme tehtävää, joista ensimmäisessä jatkavana funktiona on ensimmäisen asteen polynomi (kuvaajana suora), toisessa toisen asteen polynomi (kuvaajana paraabeli) ja kolmannessa kolmannen asteen polynomi.
1. a) Tarkista, että Tehtävä-kytkin on kohdassa 1. Funktiota 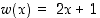 jatketaan muotoa
jatketaan muotoa 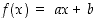 olevalla funktiolla. Etsi liukukytkimiä muuttamalla sellaiset muuttujien
olevalla funktiolla. Etsi liukukytkimiä muuttamalla sellaiset muuttujien 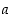 ja
ja 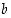 arvot, että yhteenliitetty funktio näyttäisi olevan jatkuva ja derivoituva kohdassa
arvot, että yhteenliitetty funktio näyttäisi olevan jatkuva ja derivoituva kohdassa 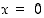 . Vastauksen näet siirtämällä Vastaus-kytkin oikealle. (Siirrä se takaisin vastauksen katsomisen jälkeen.)
. Vastauksen näet siirtämällä Vastaus-kytkin oikealle. (Siirrä se takaisin vastauksen katsomisen jälkeen.)
b) Määrää matemaattisesti laskien sellaiset muuttujien 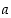 ja
ja 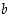 arvot, että yhteenliitetty funktio on jatkuva ja derivoituva kohdassa
arvot, että yhteenliitetty funktio on jatkuva ja derivoituva kohdassa 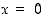 . Tarkista saitko samat arvot kuin edellisessä kohdassa.
. Tarkista saitko samat arvot kuin edellisessä kohdassa.
2. Siirrä Tehtävä-kytkin kohtaan 2. Jatkavana funktiona on nyt 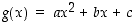 . Tutki, miten muuttujan
. Tutki, miten muuttujan 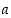 arvon vaihtaminen vaikuttaa derivoituvuuteen ja jatkuvuuteen kohdassa nolla. Millä muuttujien
arvon vaihtaminen vaikuttaa derivoituvuuteen ja jatkuvuuteen kohdassa nolla. Millä muuttujien 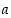 ,
,
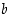 ja
ja 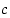 arvoilla saavutetaan jatkuvuus ja derivoituvuus nollassa?
arvoilla saavutetaan jatkuvuus ja derivoituvuus nollassa?
3. Siirrä Tehtävä-kytkin kohtaan 3. Jatkavana funktiona on nyt 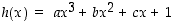 . Kuinka muuttujat
. Kuinka muuttujat 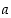 ja
ja 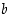 vaikuttavat jatkuvuuteen ja derivoituvuuteen nollassa? Millä muuttujien
vaikuttavat jatkuvuuteen ja derivoituvuuteen nollassa? Millä muuttujien 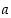 ,
,
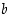 ja
ja 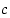 arvoilla saavutetaan jatkuvuus ja derivoituvuus nollassa?
arvoilla saavutetaan jatkuvuus ja derivoituvuus nollassa?
Tekstisijainti: Funktion sekantti ja tangentti