Derivoituvuus välillä
Funktiolla voi olla derivaatta useissa pisteissä, kuten itseisarvofunktiolla esimerkissä 3.1.1. Sanotaankin, että funktio 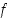 on derivoituva avoimella välillä
on derivoituva avoimella välillä 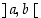 ,
jos derivaatta
,
jos derivaatta 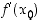 on olemassa jokaisessa välin pisteessä
on olemassa jokaisessa välin pisteessä 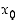 . Välin pisteissä lasketuista derivaatoista muodostuu tällöin derivaatta eli tarkemmin derivaattafunktio
. Välin pisteissä lasketuista derivaatoista muodostuu tällöin derivaatta eli tarkemmin derivaattafunktio 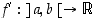 . Derivaattafunktiosta käytetään mm. merkintöjä
. Derivaattafunktiosta käytetään mm. merkintöjä
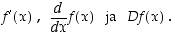
Keskimmäistä muotoa käytetään erikoisesti silloin, kun halutaan korostaa sitä, minkä muuttujan suhteen derivoidaan (varsinkin, jos funktion lausekkeessa on muitakin muuttujia kuin 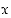 ). Muoto
). Muoto 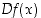 on taas käyttökelpoinen erityisesti silloin, jos funktiota ei ole nimetty tai derivointi kohdistetaan funktiolausekkeeseen.
on taas käyttökelpoinen erityisesti silloin, jos funktiota ei ole nimetty tai derivointi kohdistetaan funktiolausekkeeseen.
Esimerkki 3.2.4.
Esimerkistä 3.1.1 näkyy, että itseisarvofunktiolle 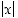 on
on 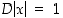 ,
kun
,
kun 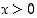 ,
ja
,
ja 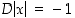 ,
kun
,
kun 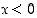 . Nollassa derivaattaa ei ole.
. Nollassa derivaattaa ei ole.

Esimerkki 3.2.5.
Esimerkin 3.1.1 todistuksesta näkyy myös se, että 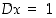 kaikkialla. Erotusosamäärän avulla on helppo osoittaa, että yleisemmin
kaikkialla. Erotusosamäärän avulla on helppo osoittaa, että yleisemmin 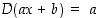 kaikkialla (kun
kaikkialla (kun 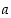 ja
ja 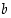 ovat vakioita). Erotusosamäärä on nimittäin vakio:
ovat vakioita). Erotusosamäärä on nimittäin vakio:
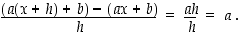

Esimerkki 3.2.6.
Esimerkin 3.1.1 mukaan itseisarvofunktio 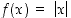 on derivoituva jokaisella sellaisella välillä, joka ei sisällä nollaa sisäpisteenään.
on derivoituva jokaisella sellaisella välillä, joka ei sisällä nollaa sisäpisteenään.
Huomaa erikoisesti, että tämän mukaan itseisarvofunktio 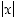 on derivoituva sekä välillä
on derivoituva sekä välillä 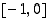 että välillä
että välillä 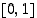 ,
mutta ei kuitenkaan koko välillä
,
mutta ei kuitenkaan koko välillä 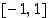 .
.

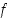 on derivoituva avoimella välillä
on derivoituva avoimella välillä 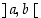 ,
jos derivaatta
,
jos derivaatta 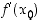 on olemassa jokaisessa välin pisteessä
on olemassa jokaisessa välin pisteessä 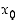 . Välin pisteissä lasketuista derivaatoista muodostuu tällöin derivaatta eli tarkemmin derivaattafunktio
. Välin pisteissä lasketuista derivaatoista muodostuu tällöin derivaatta eli tarkemmin derivaattafunktio 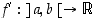 . Derivaattafunktiosta käytetään mm. merkintöjä
. Derivaattafunktiosta käytetään mm. merkintöjä 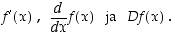
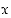 ). Muoto
). Muoto 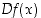 on taas käyttökelpoinen erityisesti silloin, jos funktiota ei ole nimetty tai derivointi kohdistetaan funktiolausekkeeseen.
on taas käyttökelpoinen erityisesti silloin, jos funktiota ei ole nimetty tai derivointi kohdistetaan funktiolausekkeeseen. 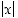 on
on 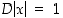 ,
kun
,
kun 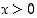 ,
ja
,
ja 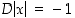 ,
kun
,
kun 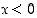 . Nollassa derivaattaa ei ole.
. Nollassa derivaattaa ei ole. 
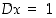 kaikkialla. Erotusosamäärän avulla on helppo osoittaa, että yleisemmin
kaikkialla. Erotusosamäärän avulla on helppo osoittaa, että yleisemmin 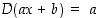 kaikkialla (kun
kaikkialla (kun 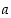 ja
ja 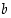 ovat vakioita). Erotusosamäärä on nimittäin vakio:
ovat vakioita). Erotusosamäärä on nimittäin vakio: 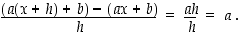

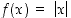 on derivoituva jokaisella sellaisella välillä, joka ei sisällä nollaa sisäpisteenään.
on derivoituva jokaisella sellaisella välillä, joka ei sisällä nollaa sisäpisteenään. 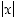 on derivoituva sekä välillä
on derivoituva sekä välillä 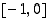 että välillä
että välillä 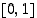 ,
mutta ei kuitenkaan koko välillä
,
mutta ei kuitenkaan koko välillä 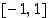 .
. 