Differentiaali ja tangenttiarvio
Differentiaalikehitelmän 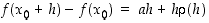 merkitys on siinä, että se antaa teoreettisen ja käytännöllisen keinon funktion arviointiin tarkastelupisteen lähistöllä. Differentiaalikehitelmässä esiintyvää termiä
merkitys on siinä, että se antaa teoreettisen ja käytännöllisen keinon funktion arviointiin tarkastelupisteen lähistöllä. Differentiaalikehitelmässä esiintyvää termiä 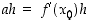 sanotaan funktion differentiaaliksi pisteessä
sanotaan funktion differentiaaliksi pisteessä 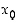 . Kehitelmä ilmaisee siis sen, että derivoituvan funktion muutosta tarkastelupisteen lähellä voidaan, lauseke
. Kehitelmä ilmaisee siis sen, että derivoituvan funktion muutosta tarkastelupisteen lähellä voidaan, lauseke 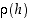 poisjättäen, arvioida derivaatan avulla eli tarkemmin sanottuna differentiaalilla. Koska pisteen
poisjättäen, arvioida derivaatan avulla eli tarkemmin sanottuna differentiaalilla. Koska pisteen 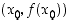 kautta kulkevan suoran, jonka kulmakerroin on
kautta kulkevan suoran, jonka kulmakerroin on 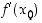 ,
yhtälö on muotoa
,
yhtälö on muotoa
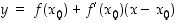 ,
,
voidaan pisteessä 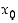 derivoituvalle funktiolle siten pisteen
derivoituvalle funktiolle siten pisteen 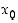 lähistöllä käyttää ns. tangenttiarviota
lähistöllä käyttää ns. tangenttiarviota
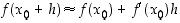 .
.
eli kyseinen tangentti on funktion
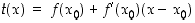
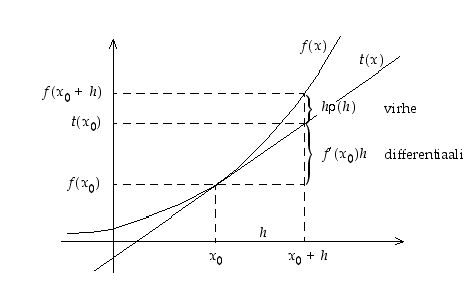
kuvaaja. Katso kuva 35.
Kuva 35.
Tangenttiarvio on sitä parempi, mitä lähempänä pistettä 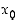 tilannetta tarkastellaaan. Differentiaalikehitelmä ei kuitenkaan anna yleistä arviota tangenttiarvion tarkkuudesta eli virheen
tilannetta tarkastellaaan. Differentiaalikehitelmä ei kuitenkaan anna yleistä arviota tangenttiarvion tarkkuudesta eli virheen 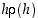 suuruudesta.
suuruudesta.
Esimerkki 3.2.3.
Esimerkin 3.2.2 mukaan funktiolla 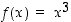 on pisteessä
on pisteessä 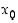 differentiaalikehitelmä
differentiaalikehitelmä
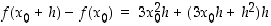
ja siten 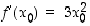 ja
ja 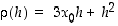 . Arvioidaan tangentin avulla arvoa
. Arvioidaan tangentin avulla arvoa 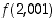 ,
kun tiedetään, että
,
kun tiedetään, että 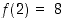 :
:
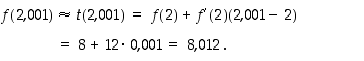
Tarkka arvo kyseisessä pisteessä on 8,012006.

Kaikki edellä olevat tarkastelut voidaan tehdä myös toispuoleisesti, joko pisteen 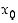 vasemmalla tai oikealla puolella. Tällaisessa tilanteessa differentiaalikehitelmä ja tangenttiarvio voivat olla siis voimassa vain toisella puolella tarkastelupistettä.
vasemmalla tai oikealla puolella. Tällaisessa tilanteessa differentiaalikehitelmä ja tangenttiarvio voivat olla siis voimassa vain toisella puolella tarkastelupistettä.
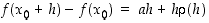 merkitys on siinä, että se antaa teoreettisen ja käytännöllisen keinon funktion arviointiin tarkastelupisteen lähistöllä. Differentiaalikehitelmässä esiintyvää termiä
merkitys on siinä, että se antaa teoreettisen ja käytännöllisen keinon funktion arviointiin tarkastelupisteen lähistöllä. Differentiaalikehitelmässä esiintyvää termiä 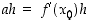 sanotaan funktion differentiaaliksi pisteessä
sanotaan funktion differentiaaliksi pisteessä 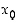 . Kehitelmä ilmaisee siis sen, että derivoituvan funktion muutosta tarkastelupisteen lähellä voidaan, lauseke
. Kehitelmä ilmaisee siis sen, että derivoituvan funktion muutosta tarkastelupisteen lähellä voidaan, lauseke 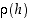 poisjättäen, arvioida derivaatan avulla eli tarkemmin sanottuna differentiaalilla. Koska pisteen
poisjättäen, arvioida derivaatan avulla eli tarkemmin sanottuna differentiaalilla. Koska pisteen 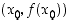 kautta kulkevan suoran, jonka kulmakerroin on
kautta kulkevan suoran, jonka kulmakerroin on 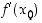 ,
yhtälö on muotoa
,
yhtälö on muotoa 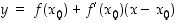 ,
,
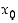 derivoituvalle funktiolle siten pisteen
derivoituvalle funktiolle siten pisteen 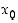 lähistöllä käyttää ns. tangenttiarviota
lähistöllä käyttää ns. tangenttiarviota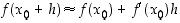 .
. 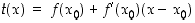
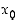 tilannetta tarkastellaaan. Differentiaalikehitelmä ei kuitenkaan anna yleistä arviota tangenttiarvion tarkkuudesta eli virheen
tilannetta tarkastellaaan. Differentiaalikehitelmä ei kuitenkaan anna yleistä arviota tangenttiarvion tarkkuudesta eli virheen 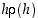 suuruudesta.
suuruudesta. 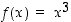 on pisteessä
on pisteessä 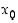 differentiaalikehitelmä
differentiaalikehitelmä 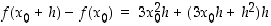
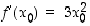 ja
ja 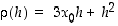 . Arvioidaan tangentin avulla arvoa
. Arvioidaan tangentin avulla arvoa 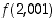 ,
kun tiedetään, että
,
kun tiedetään, että 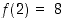 :
: 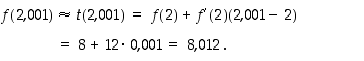

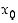 vasemmalla tai oikealla puolella. Tällaisessa tilanteessa differentiaalikehitelmä ja tangenttiarvio voivat olla siis voimassa vain toisella puolella tarkastelupistettä.
vasemmalla tai oikealla puolella. Tällaisessa tilanteessa differentiaalikehitelmä ja tangenttiarvio voivat olla siis voimassa vain toisella puolella tarkastelupistettä.