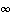 on vain symboli sille, että jokin kasvaa rajatta. Sillä ei siten saa laskea kuten luvulla. Vain sääntöjen
on vain symboli sille, että jokin kasvaa rajatta. Sillä ei siten saa laskea kuten luvulla. Vain sääntöjen
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Varsinaisille raja-arvoille aikaisemmin esitettyjä rationaalisia laskusääntöjä voidaan käyttää epäoleellisille raja-arvoillekin silloin, kun vastaan tulevat laskutoimitukset ovat tehtävissä. Muista kuitenkin, että 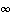 on vain symboli sille, että jokin kasvaa rajatta. Sillä ei siten saa laskea kuten luvulla. Vain sääntöjen
on vain symboli sille, että jokin kasvaa rajatta. Sillä ei siten saa laskea kuten luvulla. Vain sääntöjen
käyttö raja-arvojen yhteydessä on perusteltua. Erityisesti on huomattava, että lausekkeet
(sekä näistä äärettömän merkin vaihdolla saatavat) ovat kaikki epämääräisiä eli määrittelemättömiä. Näiden ilmentämät rajakäyttäytymiset voivat yleisesti merkitä mitä tahansa tai voi olla, että kyseistä raja-arvoa ei ole olemassakaan. Seuraavaa yksinkertaista päättelyä voi kuitenkin käyttää.
Jos (oleellisille tai epäoleellisille raja-arvoille) 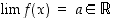 ja
ja 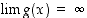 ,
niin
,
niin
(Tapaus 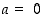 on siis epämääräinen.)
on siis epämääräinen.)
Tutkitaan ensin tilannetta, kun 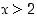 . Silloin
. Silloin
sillä 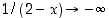 (koska
(koska 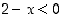 ) ja
) ja 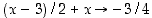 . Op. raja-arvo on siten ääretön.
. Op. raja-arvo on siten ääretön.
Vastaavasti saadaan vp. raja-arvoksi 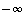 . Molemminpuolista raja-arvoa ei siten ole olemassa.
. Molemminpuolista raja-arvoa ei siten ole olemassa.
Tarkastellaan polynomifunktion 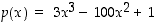 raja-arvoja äärettömyyksissä.
raja-arvoja äärettömyyksissä.
Kun 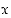 kasvaa, kasvavat polynomissa
kasvaa, kasvavat polynomissa 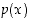 potenssit rajatta ja kyseessä on siten epämääräinen tilanne
potenssit rajatta ja kyseessä on siten epämääräinen tilanne 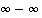 . Se huomio, että
. Se huomio, että 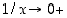 ,
kun
,
kun 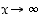 ,
saattaa joskus auttaa muuntamaan tilanteen "rationaalisemmin" pääteltäväksi. Kokeillaan sitä tässä jakamalla polynomi sopivalla muuttujan
,
saattaa joskus auttaa muuntamaan tilanteen "rationaalisemmin" pääteltäväksi. Kokeillaan sitä tässä jakamalla polynomi sopivalla muuttujan 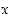 potenssilla.
potenssilla.
nähdään, että siinä 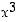 −termi lähestyy ääretöntä ja sulkulauseke lähestyy lukua 3. Siten lauseen 2.2.20 mukaan on
−termi lähestyy ääretöntä ja sulkulauseke lähestyy lukua 3. Siten lauseen 2.2.20 mukaan on
Sama tulos saadaan, kun 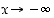 . Kumpikin raja-arvo on siten 2.
. Kumpikin raja-arvo on siten 2.
Yleensäkin rationaalifunktion käyttäytymistä äärettömyyksissä kannattaa tutkia supistamalla lauseke korkeimmalla muuttujan potenssilla. Samaa ideaa voi kokeilla muihinkin lähellä rationaalifunktioita oleviin lausekkeisiin.
Positiivisille luvuille 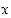 saadaan
saadaan
(Huomaa yllä olevissa muokkauksissa, että 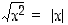 .)
.)
Havainnollistus: Testaa tietosi raja-arvosta 
Opiskeluvideo: R3: Rationaalifunktion raja-arvo 

Opiskeluvideo: R4: Neliöjuurifunktion raja-arvo 

Opiskeluvideo: R5: Epäoleelliset raja-arvot 1 

Opiskeluvideo: R6: Epäoleelliset raja-arvot 2 
