Harjoitustehtäviä

71.   Onko raja-arvoa

olemassa?

72.   Tutki lausekkeen

(eripuoleisia ja molemminpuoleisia) raja-arvoja pisteessä 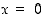. (Vihje: Lavenna sopivilla muuttujan 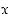monikerroilla, jotta voit käyttää lausekkeen 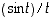raja-arvoa!)

73.   Määrää funktion

eripuoleiset raja-arvot nollassa. Onko funktiolla 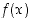raja-arvoa nollassa?

74.   Määrää

(Vihje: Tuplakulmakaavat tai lavennus summalla!)

75.   Laske laskimella lausekkeen

arvoja lähellä nollaa. Pienennä laskentapistettä aina esimerkiksi kymmenesosaan edellisestä. Mikä voisi mielestäsi olla mahdollisimman tarkka arvo lausekkeen raja-arvolle nollassa?

76.   Olkoon reaaliluvulle 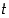luku 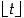suurin kokonaisluku, joka on korkeintaan 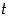(kyseessä on ns. lattiafunktio, jolle esim. 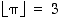ja 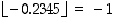). Onko funktiolla 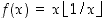toispuoleisia raja-arvoja pisteessä 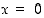? Entä muualla?

77.   Määrää

78.   Määrää

79.   Selvitä pätevätkö seuraavat päätelmät:

(a) Jos funktiolla 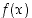on raja-arvo pisteessä 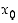, mutta funktiolla 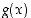ei ole, niin myöskään funktiolla 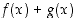ei ole.

(b) Jos funktioill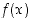a ja 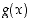ei ole kummallakaan raja-arvoa pisteessä 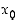, niin myöskään funktiolla 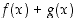ei ole.

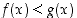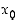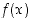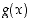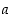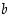80.   Selvitä päteekö seuraava päätelmä: Jos jossain pisteen sisältävällä välillä ja jos funktioilla ja on raja-arvot ja pisteessä 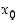, niin .

81.   Määrää raja-arvo

82.   Määrää raja-arvo

83.   Määrää raja-arvo

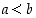84.   Yhtälöllä 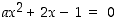on tunnetusti kaksi reaalista juurta

kun 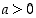. Selvitä, mitä näille kahdelle eri juurelle tapahtuu, kun .

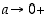85.   Oletetaan, että funktiosta 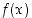tiedetään, että 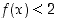aina ja että

(a) Perustele, miksi 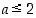. (Vihje: Muodosta vastaväite ja osoita se vääräksi.)

(b) Keksi esimerkki sellaisesta tilante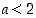esta, jossa , ja myös tilanteesta, jossa .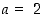

86.   Funktiosta 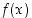tiedetään, että

Määrää raja-arvot

87.   Tason pisteen 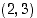kautta kulkeva suora leikkaa positiivisen 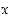−akselin pisteessä 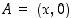ja positiivisen 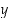−akselin pisteessä 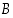. Kolmion 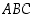kolmantena kärkenä on piste 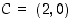. Määrää kolmion 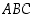ala muuttujan 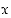avulla ja määrää sen raja-arvo, kun piste 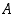lähestyy pistettä .

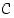88.   Tason pisteen 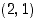kautta kulkeva suora leikkaa positiivisen 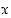−akselin pisteessä 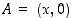ja positiivisen 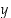−akselin pisteessä 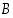. Kolmion 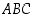kolmantena kärkenä on piste 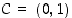. Määrää kolmion 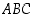ala muuttujan 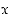avulla ja määrää sen raja-arvo, kun .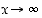