[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Polynomi tai tarkemmin polynomifunktio on mikä tahansa muotoa
oleva reaalifunktio, missä kertoimet 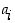 ovat reaalilukuja. Sen aste on
ovat reaalilukuja. Sen aste on 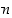 ,
kun
,
kun 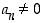 .
.
on toinen polynomi, saadaan näiden summa 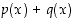 laskemalla muuttujan
laskemalla muuttujan 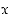 samojen potenssien kertoimet yhteen. Vastaavasti erotus
samojen potenssien kertoimet yhteen. Vastaavasti erotus 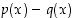 saadaan vähentämällä vastaavat kertoimet toisistaan. Edelleen polynomien
saadaan vähentämällä vastaavat kertoimet toisistaan. Edelleen polynomien 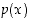 ja
ja 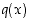 tulo
tulo 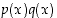 muodostetaan kertomalla lausekkeet osittelulain mukaisesti auki ja keräämällä muuttujan
muodostetaan kertomalla lausekkeet osittelulain mukaisesti auki ja keräämällä muuttujan 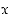 samojen potenssien kertoimet yhteen. Polynomien summat, erotukset ja tulot ovat kaikki edelleen polynomifunktioita.
samojen potenssien kertoimet yhteen. Polynomien summat, erotukset ja tulot ovat kaikki edelleen polynomifunktioita.
Polynomifunktiolle 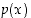 on
on 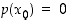 eli piste
eli piste 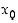 on sen nollakohta, jos ja vain jos
on sen nollakohta, jos ja vain jos 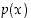 on jaollinen polynomilla
on jaollinen polynomilla 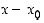 ts., jos
ts., jos
jollekin polynomille 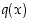 . Tämän varsin ilmeisen asian (matemaattista algebraa vaativa) todistus sivuutetaan tässä. Erityisesti kokonaislukukertoimisen polynomin
. Tämän varsin ilmeisen asian (matemaattista algebraa vaativa) todistus sivuutetaan tässä. Erityisesti kokonaislukukertoimisen polynomin
rationaalisia juuria voivat olla vain muotoa 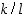 olevat luvut, missä
olevat luvut, missä 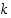 on luvun
on luvun 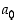 ja
ja 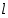 luvun
luvun 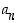 tekijä. Tämä todennetaan sijoittamalla murtoluku
tekijä. Tämä todennetaan sijoittamalla murtoluku 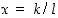 yhtälöön
yhtälöön 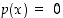 ja tarkastelemalla sitten jaollisuuksia.
ja tarkastelemalla sitten jaollisuuksia.
Kun yksi tekijä 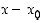 on löydetty, voidaan toinen tekijä
on löydetty, voidaan toinen tekijä 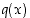 laskea seuraavan esimerkin mukaisesti jakokulman avulla. Yleisesti rationaalikertoimisen polynomin
laskea seuraavan esimerkin mukaisesti jakokulman avulla. Yleisesti rationaalikertoimisen polynomin
rationaaliset juuret voivat olla muotoa 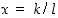 ,
missä
,
missä 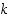 on luvun
on luvun 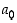 ja
ja 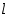 luvun
luvun 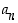 tekijä.
tekijä.
Polynomin 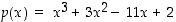 mahdolliset rationaaliset juuret ovat
mahdolliset rationaaliset juuret ovat 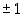 ja
ja 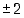 . Kokeilemalla on helppo todeta, että
. Kokeilemalla on helppo todeta, että 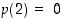 ,
joten sillä on tekijänä polynomi
,
joten sillä on tekijänä polynomi 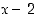 . Määrätään toinen tekijä jakokulmalla.
. Määrätään toinen tekijä jakokulmalla.
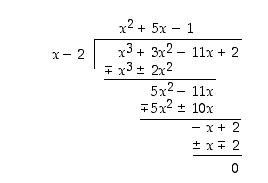
Siten 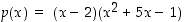 . Tarkista tulos kertomalla saadut tekijäpolynomit.
. Tarkista tulos kertomalla saadut tekijäpolynomit.
Opiskeluvideo: F8: Polynomin jako tekijöihin jakokulmalla 

Polynomien muokkauksia varten on hyödyllistä muistaa binomikaava eli summan neliön kaava
summan ja erotuksen tulosääntö
ja toisen asteen polynomin juurikaava
Toisen asteen polynomilla on siis reaalisia juuria vain, jos sen diskriminantti 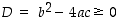 . Jos
. Jos 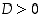 ,
on polynomilla kaksi eri juurta, ja jos
,
on polynomilla kaksi eri juurta, ja jos 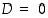 ,
on sillä täsmälleen yksi juuri. Edellä oleva juurikaava voidaan johtaa "neliöimällä" yhtälön vasen puoli:
,
on sillä täsmälleen yksi juuri. Edellä oleva juurikaava voidaan johtaa "neliöimällä" yhtälön vasen puoli:
Edellä olevassa esimerkissä 1.5.10 määrätyllä tekijäpolynomilla 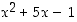 on juuret
on juuret
Opiskelutehtävä 6. (Polynomin juuri)
Määritä sellainen vakio 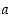 ,
että polynomilla
,
että polynomilla 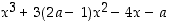 on juurena luku
on juurena luku 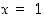 . Mitkä ovat tällöin muut juuret?
. Mitkä ovat tällöin muut juuret?
Havainnollistus: Toisen asteen käyrän sovittaminen 
Laskentapohja: Arvaa funktio 1 
Laskentapohja: Arvaa funktio 2 
Laskentapohja: Arvaa funktio 3 
Laskentapohja: Arvaa funktio 4 
Laskentapohja: Arvaa funktio 5 
Laskentapohja: Arvaa funktio 6 