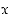 asetetaan
asetetaan 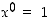 ,
,
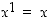 ja yleisemmin induktiivisesti
ja yleisemmin induktiivisesti 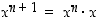 ,
kun
,
kun 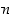 on luonnollinen luku. Erityisesti sovitaan lisäksi, että
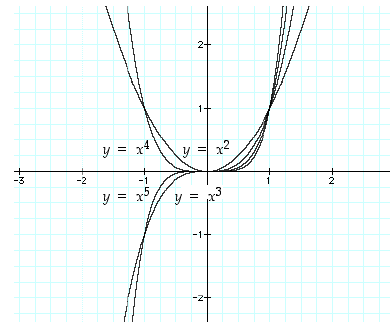
on luonnollinen luku. Erityisesti sovitaan lisäksi, että 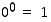 . Kuvassa 15 on potenssifunktioiden
. Kuvassa 15 on potenssifunktioiden 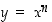 kuvaajia, kun
kuvaajia, kun 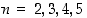 .
.
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Yleinen (kokonaislukupotenssinen) potenssifunktio määritellään seuraavasti. Reaaliluvulle 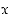 asetetaan
asetetaan 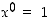 ,
,
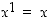 ja yleisemmin induktiivisesti
ja yleisemmin induktiivisesti 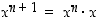 ,
kun
,
kun 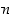 on luonnollinen luku. Erityisesti sovitaan lisäksi, että
on luonnollinen luku. Erityisesti sovitaan lisäksi, että 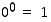 . Kuvassa 15 on potenssifunktioiden
. Kuvassa 15 on potenssifunktioiden 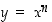 kuvaajia, kun
kuvaajia, kun 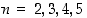 .
.
Luvuille 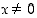 asetetaan edelleen
asetetaan edelleen 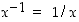 ja yleisemmin
ja yleisemmin
kun 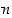 on positiivinen kokonaisluku. Tällöin negatiiviset potenssit tulevat määriteltyä myös induktiivisesti:
on positiivinen kokonaisluku. Tällöin negatiiviset potenssit tulevat määriteltyä myös induktiivisesti: 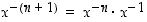 ,
kun
,
kun 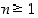 ja
ja 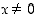 . Merkinnässä
. Merkinnässä 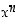 luku
luku 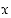 on kantaluku ja luku
on kantaluku ja luku 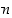 on potenssi. Näin määritellyille kokonaislukupotensseille ovat seuraavat laskulait voimassa:
on potenssi. Näin määritellyille kokonaislukupotensseille ovat seuraavat laskulait voimassa:
kun 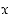 ,
,
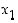 ja
ja 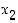 ovat reaalilukuja (ja nollasta eroavia, mikäli jokin potenssi on negatiivinen) sekä
ovat reaalilukuja (ja nollasta eroavia, mikäli jokin potenssi on negatiivinen) sekä 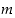 ja
ja 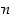 ovat kokonaislukuja.
ovat kokonaislukuja.
Potenssifunktion 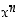 ,
missä
,
missä 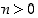 ,
käänteiskuvaus on juurifunktio
,
käänteiskuvaus on juurifunktio 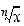 . Se määräytyy siis siitä, että ehto
. Se määräytyy siis siitä, että ehto 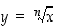 pätee täsmälleen silloin, kun
pätee täsmälleen silloin, kun 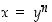 . Jos potenssi
. Jos potenssi 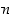 on pariton kokonaisluku, on juurifunktio määritelty kaikille reaaliluvuille
on pariton kokonaisluku, on juurifunktio määritelty kaikille reaaliluvuille 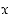 ja sen arvo on samanmerkkinen kuin luku
ja sen arvo on samanmerkkinen kuin luku 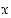 ,
mutta jos
,
mutta jos 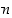 on parillinen, on juurifunktio määritelty vain epänegatiivisille luvuille
on parillinen, on juurifunktio määritelty vain epänegatiivisille luvuille 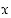 ja sen arvo on silloin epänegatiivinen. Merkinnässä
ja sen arvo on silloin epänegatiivinen. Merkinnässä 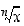 luku
luku 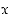 on juurrettava ja luku
on juurrettava ja luku 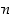 on indeksi. Juurifunktiolle käytetään myös potenssimaista merkintää
on indeksi. Juurifunktiolle käytetään myös potenssimaista merkintää 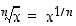 ,
kun
,
kun 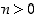 . Kuvassa 16 ovat potenssifunktioiden
. Kuvassa 16 ovat potenssifunktioiden 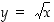 ja
ja 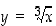 kuvaajat.
kuvaajat.
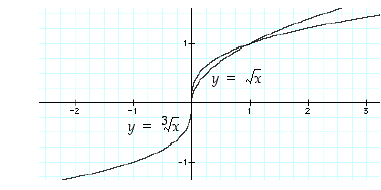
Kun sovitaan lisäksi, että kokonaisluvuille 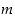 ja
ja 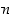 ,
missä
,
missä 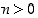 ,
on
,
on
on saatu määriteltyä yleiset rationaalipotenssit eli potenssit 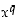 ,
missä
,
missä 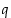 on rationaaliluku. Näille rationaalipotensseille ovat laskulait
on rationaaliluku. Näille rationaalipotensseille ovat laskulait
voimassa aina, kun 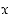 ,
,
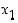 ja
ja 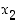 ovat positiivisia reaalilukuja sekä
ovat positiivisia reaalilukuja sekä 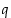 ja
ja 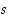 ovat rationaalilukuja. Sellaiset murtopotenssit
ovat rationaalilukuja. Sellaiset murtopotenssit 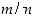 ,
jotka ovat supistetussa muodossa ja joissa
,
jotka ovat supistetussa muodossa ja joissa 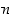 on pariton, voidaan määritellä myös negatiivisille luvuille
on pariton, voidaan määritellä myös negatiivisille luvuille 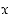 ,
mutta näille edellä olevat laskulait eivät välttämättä ole enää voimassa. Esimerkiksi
,
mutta näille edellä olevat laskulait eivät välttämättä ole enää voimassa. Esimerkiksi 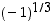 ja
ja 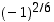 antavat eri tuloksen.
antavat eri tuloksen.
Irrationaalisille potensseille 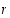 lauseke
lauseke 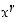 määritellään vasta myöhemmin eksponenttifunktioiden yhteydessä pykälässä Eksponenttifunktio.
määritellään vasta myöhemmin eksponenttifunktioiden yhteydessä pykälässä Eksponenttifunktio.