[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Rationaalifunktio on kahden polynomin osamäärästä muodostuva funktio. Sen lauseke on näin ollen muotoa
missä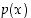 
ja 
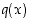ovat polynomeja. Se on määritelty niissä piste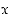issä 
,
joissa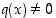 
.
Jos rationaalifunktion osoittaja- ja nimittäjäpolynomeilla on yhteisiä juuria tai yleisemmin yhteisiä polynomitekijöitä, voidaan nämä yhteiset tekijät supistaa pois. On kuitenkin huomattava, että itse funktion määrittelyjoukko saattaa silloin muuttua, jolloin koko funktiokin muuttuu periaatteessa eri funktioksi.
ei ole määritelty, kun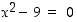 
eli kun 
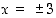. Kun huomataan, että osoittajalla ja nimittäjällä on yhteinen tekijä 
,
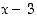funktion lauseke voidaan supistaa muotoon
joka onkin nyt määritelty myös kohdassa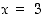 
. Tarkkaan ottaen supistettu lauseke määrittelee uuden funktion, koska sen määrittelyalue on muuttunut. On syytä pitäytyä siinä, että funktion 
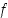määrittelyjoukko on se, mikä alkuperäisestä lausekkeesta määräytyy. Näin ollen 
.
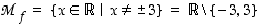Rationaalifunktioiden summat, erotukset, tulot ja osamäärät (niissä pisteissä, joissa osamäärä voidaan laskea) eli yleisemmin ilmaistuna rationaalifunktioiden rationaaliset lausekkeet ovat edelleen rationaalifunktioita. Tällaisia rationaalisia lausekkeita voidaan muokata samoin säännöin kuin rationaalilukuja (ks. Rationaaliluku). Rationaalifunktion lausekkeen ei siten tarvitse välttämättä olla polynomien osamäärämuodossa − riittää, että lausekkeessa esiintyy vain polynomeja sekä (mahdollisesti toistuvasti) niiden summia, erotuksia, tuloja ja osamääriä.
Huomaa, että saatu lauseke on määritelty myös pisteissä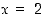 
ja 
,
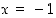vaikka molempia tekijöitä ei ole näissä pisteissä määritelty eikä itse tuloa näin ollen voi muodostaa näissä pisteissä.
lauseke muodostuu polynomeista ja niiden summista, erotuksista, tuloista ja osamääristä. Se on siten rationaalifunktio. Itse asiassa sen lauseke voidaan laventaa esimerkiksi muotoon
mistä lausekkeen rationaalisuus eli kahden polynomin osamäärämuoto näkyykin selvästi.
