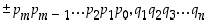Desimaaliluku

Rationaaliluvut voidaan täydentää reaaliluvuiksi myös käyttäen jonojen teoriaa hyväksi, jolloin reaaliluvut tulevat olemaan suppenevien rationaalilukujonojen raja-arvoja. Tällaiseen perustuu mm. seuraavassa käsiteltävä reaalilukujen esitys desimaalilukuna.

Reaaliluvut voidaan käsittää kymmenjärjestelmässä esitetyiksi desimaaliluvuiksi. Päättyvä desimaaliluku on yleisesti muotoa

,

missä luvut 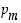, ..., 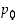ja 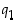, ..., 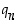ovat kokonaislukuja väliltä 0−9. Sen kokonaisosa on kokonaisluku

ja desimaaliosa on luku

.

On selvää, että tämä desimaaliosa ja siten myös koko päättyvä desimaaliluku on rationaaliluku (lavenna lausekkeet luvulla ).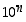

Päättymätön desimaaliluku on taas muotoa

,

missä mistään indeksistä 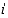alkaen luvut 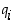eivät ole kaikki nollia. Desimaaliosan pituutta ei siis ole nyt mitenkään rajattu. (Jos päättymättömässä desimaaliluvussa desimaaliosan luvut ovat jostain indeksistä alkaen kaikki nollia, luku onkin itse asiassa päättyvä desimaaliluku!) Tämän luvun desimaaliosa 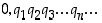tarkoittaa itse asiassa loputtoman summauksen eli sarjan

summaa. Sen osoittamiseksi, että tämä loputon summaus on mielekäs ja antaa todella jonkun reaaliluvun tuloksena, tarvitaan mm. reaalilukujen täydellisyyttä (ks. Reaalilukujen täydellisyys) ja sarjojen suppenemisteoriaa. Tarkempi käsittely sivuutetaan tässä teoksessa.

Rationaaliluvun desimaaliesitys on yleistä reaaliluvun esitystä helpompi selvittää. Se voi tietenkin olla päättyvä, kuten e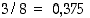simerkiksi , mutta se voi olla myös päättymätön, kuten esimerkiksi 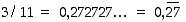. Tässä merkinnässä viiva desimaaliosan päällä merkitsee sitä, että kyseinen numerosarja toistuu loputtomasti. Tällaista desimaalilukua sanotaan jaksolliseksi ja toistuva numerosarja on sen jakso.

Toisaalta päättyvät desimaaliluvut ovat, kuten edellä todettiin, rationaalilukuja. Myös jaksolliset desimaaliluvut ovat rationaalilukuja, mistä seuraava esimerkki antaa kuvan.

Esimerkki 1.3.3.

Osoitetaan, että jaksollinen desimaaliluku 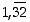on rationaaliluku. Tehdään se kahdella tavalla, ensin löysemmin perustein ja sitten matemaattisesti perustellummin.

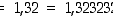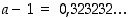(a)  Kun merkitään, että , on ja

.

Siten 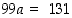, josta 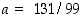. Tämä ratkaisu on siinä mielessä epätäsmällinen, että ei ole ilman muuta selvää, miten päättymättömillä desimaaliluvuilla voidaan laskea. Tämän selvittämiseen tarvitaan sarjateoriaa.

(b)  Käytetään hyväksi geometrisen sarjan summakaavaa, jonka mukaan

kun sarjan (eli loputtoman summauksen) peräkkäisten termien suhteelle 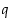pätee, että 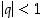. Luku 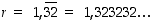tarkoittaakin nyt oikeasti sarjaa

joten geometrisen sarjan summakaavan mukaan

Opiskelutehtävä 2. (Desimaaliluku)

Muuta desimaaliluvut 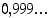ja 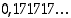rationaaliluvuiksi.

Vinkki tehtävään 2

Jaksolliset desimaaliluvut voidaan muuttaa rationaaliluvuiksi käyttäen geometrisia sarjoja hyväksi, kuten edellisen esimerkin (b)-kohta kuvaa. Yleisemmän menettelyn osalta katso myös harjoitustehtävä 17. Seuraava tulos näin ollen pätee.

Lause 1.3.4.

Rationaaliluvun desimaaliesitys on päättyvä tai jaksollinen. Toisaalta päättyvät ja jaksolliset desimaaliluvut ovat rationaalilukuja.

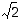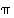Irrationaaliluvuilla, kuten esimerkiksi luvulla , ei näin ollen voi olla jaksollisia desimaaliesityksiä. Myöskään lukujen ja 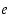desimaaliesityksistä ei ole löydettävissä mitään jaksoa, sillä ne ovat transkendenttisinä lukuina myös irrationaalisia.