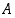 on pienin yläraja
on pienin yläraja 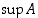 .
.
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Ei ole matemaattisesti itsestään selvää, että jokaisella reaalilukujoukolla olisi supremum tai infimum. Reaalilukujen erilaisten konstruktioiden (Dedekindin leikkausten tai suppenevien rationaalilukujonojen) avulla voidaan kuitenkin osoittaa, että rajoitetuilla joukoilla nämä ovat olemassa. Oletamme sen tässä kuitenkin annettuna tosiasiana.
Aksiooma 1.3.11. (Reaalilukujen täydellisyysaksiooma)
Jokaisella epätyhjällä, ylhäältä rajoitetulla reaalilukujoukolla 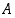 on pienin yläraja
on pienin yläraja 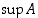 .
.
Tarkastelemalla reaalilukujen päinvastaista järjestystä päätellään edellä olevasta aksioomasta seuraava tulos.
Jokaisella epätyhjällä, alhaalta rajoitetulla reaalilukujoukolla 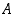 on suurin alaraja
on suurin alaraja 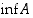 .
.
Joukko 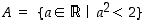 on ylhäältä rajoitettu kuten esimerkissä 1.3.7 todettiin. Se ei selvästikään ole tyhjä joukko, joten täydellisyysaksiooman mukaan on olemassa
on ylhäältä rajoitettu kuten esimerkissä 1.3.7 todettiin. Se ei selvästikään ole tyhjä joukko, joten täydellisyysaksiooman mukaan on olemassa 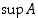 . Itse asiassa
. Itse asiassa 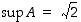 . Osoitetaan se, ts. osoitetaan, että luvulle
. Osoitetaan se, ts. osoitetaan, että luvulle 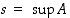 on
on 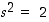 . Tämä taas voidaan osoittaa kumoamalla ehdot
. Tämä taas voidaan osoittaa kumoamalla ehdot 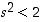 ja
ja 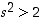 .
.
Koska 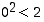 voidaan olettaa, että
voidaan olettaa, että 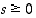 . Valitaan avuksi toinen luku
. Valitaan avuksi toinen luku
Oletetaan ensin, että 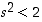 . Tällöin
. Tällöin 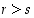 ,
sillä edellisen yhtälön mukaan on
,
sillä edellisen yhtälön mukaan on 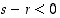 . Toisaalta
. Toisaalta 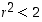 ,
sillä jälkimmäisen yhtälön mukaan on
,
sillä jälkimmäisen yhtälön mukaan on 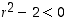 . Siten
. Siten 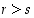 ja
ja 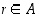 ,
mikä on vastoin ehtoa
,
mikä on vastoin ehtoa 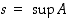 .
.
Jos taas 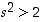 ,
niin
,
niin 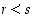 ,
sillä nyt
,
sillä nyt 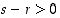 ,
ja toisaalta
,
ja toisaalta 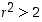 ,
sillä nyt
,
sillä nyt 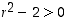 . Siten kaikille luvuille
. Siten kaikille luvuille 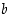 ,
joille
,
joille 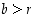 ,
on
,
on 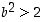 . Näiden lukujen joukossa ei siten voi olla yhtään joukon
. Näiden lukujen joukossa ei siten voi olla yhtään joukon 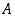 alkiota. Tämä on ristiriidassa lauseen 1.3.8 kohdan (2) kanssa.
alkiota. Tämä on ristiriidassa lauseen 1.3.8 kohdan (2) kanssa.
Molemmissa tapauksissa saadut tulokset ovat siten ristiriidassa sen kanssa, että 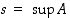 . Siispä
. Siispä 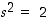 ,
kun
,
kun 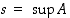 .
.
Vastaavasti voidaan osoittaa, että 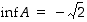 .
.
Tämä esimerkki osoittaa samalla, että rationaalilukujen joukolla ei ole vielä täydellisyysominaisuutta. Rationaalilukujoukolle 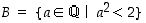 on nimittäin myös
on nimittäin myös 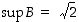 ja toisaalta aikaisemmin esimerkissä 1.3.1 osoitettiin, että
ja toisaalta aikaisemmin esimerkissä 1.3.1 osoitettiin, että 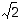 ei ole rationaalinen luku. Joukolla
ei ole rationaalinen luku. Joukolla 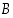 ei siten ole rationaalilukua supremumina.
ei siten ole rationaalilukua supremumina.