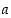 ,
,
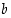 ja
ja 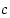 ovat joko kaikki rationaalilukuja tai kaikki reaalilukuja.
ovat joko kaikki rationaalilukuja tai kaikki reaalilukuja.
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Rationaali- ja reaalilukujen perusominaisuudet eli aksioomat voidaan ryhmitellä yhteenlaskua, kertolaskua ja järjestystä koskeviin ominaisuuksiin. Seuraavissa ehdoissa esiintyvät luvut 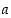 ,
,
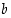 ja
ja 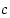 ovat joko kaikki rationaalilukuja tai kaikki reaalilukuja.
ovat joko kaikki rationaalilukuja tai kaikki reaalilukuja.
I. Yhteenlaskuominaisuudet, jotka sisältävät yhteenlaskua koskevat laskulait:
II. Kertolaskuominaisuudet, jotka sisältävät kertolaskua koskevat laskulait:
(d) Käänteisluvun 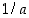 olemassaolo:
olemassaolo: 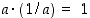 ,
kun
,
kun 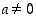 .
.
III. Järjestysominaisuudet,
jotka määräytyvät positiivisuuden (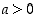 ) perusteella:
) perusteella:
(a) Kolmijakoisuus: Luvulle 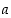 on joko
on joko 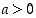 ,
,
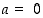 tai
tai 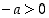 (toistensa poissulkevasti).
(toistensa poissulkevasti).
(b) Säilymislait: Kun 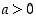 ja
ja 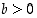 ,
niin myös
,
niin myös 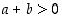 ja
ja 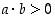 .
.
Opiskelutehtävä 3. (Käänteisluku)
Osoita, että luku 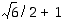 on luvun
on luvun 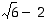 käänteisluku.
käänteisluku.
Lukujen 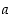 ja
ja 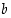 erotus on
erotus on 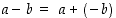 ja vastaavasti osamäärä on
ja vastaavasti osamäärä on 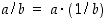 ,
kun
,
kun 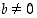 . Kertolaskussa ei yleisesti käytetä muuttujien yhteydessä pistettä, merkitään siis
. Kertolaskussa ei yleisesti käytetä muuttujien yhteydessä pistettä, merkitään siis 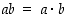 .
.
Yleinen järjestys määritellään asettamalla 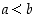 ,
kun
,
kun 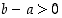 . Luvut
. Luvut 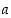 ,
joille
,
joille 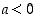 ,
ovat negatiivisia. Merkintä
,
ovat negatiivisia. Merkintä 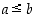 tarkoittaa, että
tarkoittaa, että 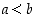 tai
tai 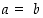 .
.
Edellä olevien aksioomien lisäksi reaaliluvuilla on yksi ominaisuus, jota ei rationaaliluvuille ole, nimittäin ns. täydellisyysominaisuus. Se muotoillaan kohdassa 1.3.11. Ennen sitä tarkastellaan seuraavassa tähän tarvittavia käsitteitä.