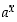 kantaluvuksi valitaan Neperin luku
kantaluvuksi valitaan Neperin luku 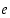 ,
saadaan (luonnollinen tai tavallinen) eksponenttifunktio
,
saadaan (luonnollinen tai tavallinen) eksponenttifunktio 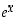 . Se on määritelty kaikilla reaaliluvuilla ja sen arvo määräytyy siis lausekkeesta
. Se on määritelty kaikilla reaaliluvuilla ja sen arvo määräytyy siis lausekkeesta
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Kun yleisen eksponenttifunktion 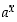 kantaluvuksi valitaan Neperin luku
kantaluvuksi valitaan Neperin luku 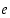 ,
saadaan (luonnollinen tai tavallinen) eksponenttifunktio
,
saadaan (luonnollinen tai tavallinen) eksponenttifunktio 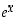 . Se on määritelty kaikilla reaaliluvuilla ja sen arvo määräytyy siis lausekkeesta
. Se on määritelty kaikilla reaaliluvuilla ja sen arvo määräytyy siis lausekkeesta
Erityisesti 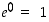 ja
ja 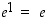 . Eksponenttifunktiosta käytetään myös merkintää
. Eksponenttifunktiosta käytetään myös merkintää 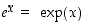 .
.
Eksponenttifunktiolla on seuraavat erityiset ominaisuudet.
Eksponenttifunktiolle 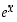 ovat seuraavat voimassa.
ovat seuraavat voimassa.
(c) 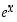 on kaikkialla aidosti kasvava,
on kaikkialla aidosti kasvava,
Todistus. (a) Väite on yleisen reaalilukupotenssin supremum-määrittelyn perusteella ilmeinen, mutta sen täsmällinen matemaattinen todistus sivuutetaan tässä.
(b) Koska luku 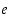 on positiivinen, on
on positiivinen, on 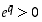 kaikille rationaaliluvuille
kaikille rationaaliluvuille 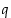 . Määritelmän mukaisesti on siten myös
. Määritelmän mukaisesti on siten myös 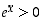 . Jos sitten
. Jos sitten 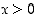 ,
on
,
on 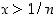 jollekin positiiviselle kokonaisluvulle
jollekin positiiviselle kokonaisluvulle 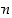 ja siten määrittelyn perusteella
ja siten määrittelyn perusteella 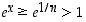 .
.
(c) Kun 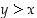 ,
on
,
on 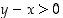 ja siten edellisen kohdan mukaan
ja siten edellisen kohdan mukaan 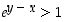 . Näin ollen
. Näin ollen
(d) Koska 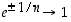 ,
kun
,
kun 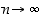 ,
niin myös
,
niin myös 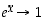 ,
kun
,
kun 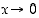 . Tämän perusteella yleisemmin
. Tämän perusteella yleisemmin
Funktio 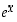 on siten kaikkialla jatkuva.
on siten kaikkialla jatkuva.
(e) (Tämän kohdan todistus on näistä kohdista pisin ja teknisin.) Määrätään ensin derivaatta nollassa eli erotusosamäärän raja-arvo
Kun 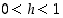 ,
niin
,
niin 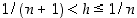 jollekin kokonaisluvulle
jollekin kokonaisluvulle 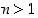 . Toisaalta kaikille
. Toisaalta kaikille 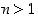 on
on
Yhdistämällä kaikki edellä olevat arviot saadaan arvioketju
Kun nyt 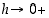 ,
niin
,
niin 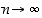 . Edellä olevassa arviossa laitimmaisten lausekkeiden raja-arvot ovat ykkösiä (kun
. Edellä olevassa arviossa laitimmaisten lausekkeiden raja-arvot ovat ykkösiä (kun 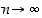 ), joten kuristuslauseen mukaan
), joten kuristuslauseen mukaan
Vastaava vasemmanpuoleinen raja-arvo saadaan yhtä suureksi tekemällä edellä saatuun tulokseen merkin vaihto:
Funktion 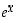 derivaatta nollassa on siten yksi.
derivaatta nollassa on siten yksi.
Derivaatta muissa pisteissä saadaan tämän jälkeen siirtämällä yleisen erotusosamäärän tarkastelu edellä olevaan tilanteeseen seuraavasti.
(f) Kun 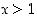 ,
on
,
on 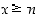 jollekin kokonaisluvulle
jollekin kokonaisluvulle 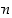 . Koska
. Koska 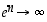 ,
kun
,
kun 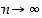 (sillä
(sillä 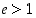 ), niin myös
), niin myös 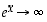 ,
kun
,
kun 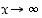 .
.
Jos sitten 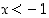 ,
on
,
on 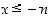 jollekin kokonaisluvulle
jollekin kokonaisluvulle 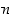 ja siten
ja siten
Eksponenttifunktion kuvaaja on kuvassa 55.
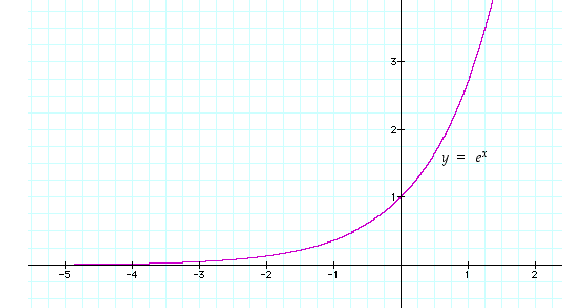
Kuva 55. Eksponenttifunktion kuvaaja
Havainnollistus: Eksponenttifunktio 
Määrätään lausekkeen 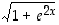 derivaatta:
derivaatta:
Osoitetaan, että eksponenttifunktion kuvaaja sivuaa suoraa 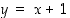 ja on muulloin sen yläpuolella.
ja on muulloin sen yläpuolella.
Yhtälöllä 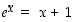 on ratkaisuna ainakin
on ratkaisuna ainakin 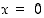 . Pitää siis osoittaa, että
. Pitää siis osoittaa, että 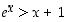 ,
kun
,
kun 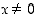 . Funktiolle
. Funktiolle 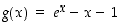 on
on 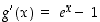 . Lauseen 6.1.2 kohdan (b) mukaan on
. Lauseen 6.1.2 kohdan (b) mukaan on 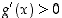 ,
kun
,
kun 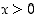 . Siten
. Siten 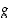 on aidosti kasvava, kun
on aidosti kasvava, kun 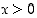 . Näin ollen
. Näin ollen 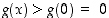 kun
kun 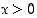 . Yhtälö
. Yhtälö 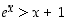 toteutuu siis ainakin, kun
toteutuu siis ainakin, kun 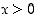 .
.
Kun 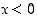 ,
on
,
on 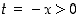 ja siten edellisen tarkastelun mukaan
ja siten edellisen tarkastelun mukaan
Funktio 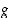 on näin ollen aidosti vähenevä, kun
on näin ollen aidosti vähenevä, kun 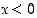 . Siten
. Siten 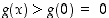 kun
kun 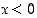 . Yhtälö
. Yhtälö 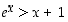 toteutuu täten myös, kun
toteutuu täten myös, kun 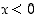 .
.
Tuloksena on siten, että suora 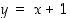 on eksponenttifunktion tangentti pisteessä
on eksponenttifunktion tangentti pisteessä 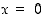 ja funktion kuvaaja on muuten tämän suoran yläpuolella.
ja funktion kuvaaja on muuten tämän suoran yläpuolella.
Seuraavassa pykälässä logaritmifunktion yhteydessä määrätään yleisen eksponenttifunktion 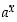 derivaatta (ks. Yleinen eksponenttifunktio ja logaritmifunktio).
derivaatta (ks. Yleinen eksponenttifunktio ja logaritmifunktio).
Tavallisen eksponenttifunktion 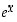 tekee "luonnolliseksi" se, että sen derivaattafunktio on täsmälleen se itse. Erityisesti
tekee "luonnolliseksi" se, että sen derivaattafunktio on täsmälleen se itse. Erityisesti 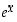 tämän mukaan kasvaa "kiihtyvällä nopeudella", ts. se kasvaa sitä nopeammin, mitä suurempi sen arvo jo on.
tämän mukaan kasvaa "kiihtyvällä nopeudella", ts. se kasvaa sitä nopeammin, mitä suurempi sen arvo jo on.