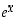Eksponenttifunktion kasvunopeus

Edellä olevan mukaan eksponenttifunktio 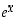kasvaa "kiihtyvällä nopeudella", ts. se kasvaa sitä nopeammin, mitä suurempi sen arvo jo on. Seuraava tulos osoittaa, että se kasvaa jopa nopeammin kuin mikään potenssifunktio.

Lause 6.1.5.

Kaikille kokonaisluvuille on

Todistus. Funktiolle

on ensimmäinen derivaatta

ja toinen derivaatta

Siten derivaatta 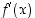on kasvava, kun 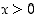. Edelleen, kun 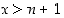, on väliarvolauseen mukaan

jollekin 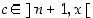. Koska 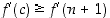, saadaan arvio

.

Tässä 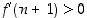, joten arvion oikean puolen raja-arvo on ääretön, kun 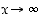(luku 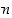on nyt nimittäin vakio). Siten myös .

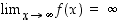Pykälän alussa todettiin, että luvut 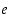ja 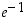saadaan eräiden lukujonojen raja-arvoina. Seuraava tulos osoittaa, että ne saadaan myös kyseisistä jonoista muodostettujen funktioiden raja-arvoina. Seuraavassa lauseessa esiintyvät lausekkeet, joissa sekä kantaluku että potenssi ovat muuttuvia, tulevat tosin perusteltua vasta logaritmifunktion yhteydessä (ks. Yleinen eksponenttifunktio ja logaritmifunktio). Tässä käytetään hyväksi sitä, että tällaisiakin lausekkeita voidaan muokata kuten potenssi- ja eksponenttifunktioita.

Opiskelutehtävä 32. (Eksponenttifunktion käyttäytyminen)

Määritä funktion 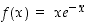ääriarvot, käännepisteet ja asymptootit. Hahmottele kuvaajaa.

Vinkki tehtävään 32

Lause 6.1.6.

Todistus. Kun 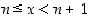, saadaan potenssi- ja eksponenttifunktioiden aidon kasvavuuden perusteella seuraava arvioketju

Tässä vasemmanpuoleisin lauseke voidaan kirjoittaa muotoon

missä 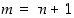. Tästä nähdään, että tämän lausekkeen raja-arvo o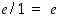n , kun 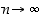(jolloin tietenkin myös 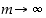). Vastaavasti eo. arvioketjun oikeanpuoleisin lauseke on muotoa

mistä nähdään, että sen raja-arvo o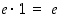n , kun 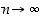. Siten kuristuslauseen mukaan näitten välissä olevan lausekkeen

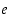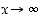raja-arvo on sama luku , sillä kun , niin myös .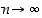

Väitteen toinen tulos todistetaan vastaavasti.