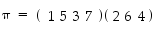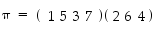Tehtävä 5.6. Määrää permutaatiolle käänteispermutaatio ja esitä se erillisten kiertojen tulona.

Ratkaisu

Ratkaisutapa I. Yksi tapa etsiä permutaation 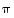käänteispermutaatio on kirjoittaa erillisten kiertojen tulo kaksirivisenä esityksenä, vaihtaa kaksirivisen esityksen rivit toisikseen ja järjestää ylärivi kasvavaan järjestykseen: Koska

niin

Ratkaisutapa II. Yhden kierron 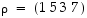käänteispermutaatio saadaan selville käymällä läpi kuvautumiset seuraavasti: 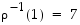, , 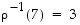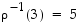ja 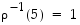. Näin ollen 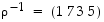. Samalla tavalla huomataan, että 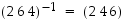. Siten käänteispermutaatio 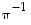esitettynä erillisten kiertojen tulona on .

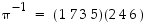Lisätietoja. Huomaa, että esimerkiksi kierrot (2 4 6), (6 2 4) ja (4 6 2) ovat eri esityksiä täsmälleen samalle kierrolle, jossa kakkonen kuvautuu neloseksi, nelonen kuutoseksi ja kuutonen kakkoseksi. Havaitaan, että näistä esityksistä (4 6 2) on alkuperäinen kierto (2 6 4) käännetyssä järjestyksessä. Vastaavasti .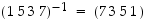

Kahden erillisen kierron tulon käänteispermutaatio saadaan nyt 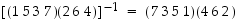. Tässä kiertojen erillisyys on olennaista, sillä yleensä permutaatioille on 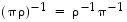, ts. myös kertomisjärjestys vaihtuu. Erilliset kierrot voidaan kuitenkin kertoa missä järjestyksessä tahansa.

Näin ollen yleisesti permutaation käänteispermutaatio voidaan löytää sen erillisten kiertojen esityksestä nopeasti vaihtamalla vain jokaisessa kierrossa luvut vastakkaiseen järjestykseen.

[Opiskelutehtäviä 5]