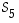 ? Entä sellaista, jotka kuvaavat joko alkiot 1 ja 2 molemmat itselleen tai molemmat toisikseen?
? Entä sellaista, jotka kuvaavat joko alkiot 1 ja 2 molemmat itselleen tai molemmat toisikseen? 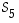 ? Entä sellaista, jotka kuvaavat joko alkiot 1 ja 2 molemmat itselleen tai molemmat toisikseen?
? Entä sellaista, jotka kuvaavat joko alkiot 1 ja 2 molemmat itselleen tai molemmat toisikseen?
b) Yleistyksenä ilmoita edelleen, kuinka monta sellaista permutaatiota, jotka kuvaavat
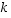 ensimmäistä alkiota kaikki itselleen, on ryhmässä
ensimmäistä alkiota kaikki itselleen, on ryhmässä 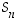 ? Entä sellaista, jotka kuvaavat ne joko itselleen tai toisikseen?
? Entä sellaista, jotka kuvaavat ne joko itselleen tai toisikseen?
a) Tehtävä voidaan selvittää joko kirjoittamalla auki permutaatioiden kaksirivisiä muotoja ja miettimällä mitä termejä toisella rivillä voi missäkin kohdassa olla tai käyttämällä suoraan kertomamerkintöjä, mikäli tämä tuntuu tutulta.
i) Sellaiselle permutaatiolle, joka kuvaa alkion 1 itselleen täytyy päteä
Näin ollen kuvauksen ensimmäinen kuvautuminen (ensimmäinen tulos) voidaan valita vain yhdellä tavalla. Toinen termi 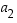 voidaan valita neljän jäljellä olevan alkion joukosta eli joukosta
voidaan valita neljän jäljellä olevan alkion joukosta eli joukosta 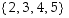 .
Sen jälkeen paikkaan
.
Sen jälkeen paikkaan 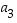 voidaan valita alkio kolmella tavalla. Näin jatkamalla havaitaan, että erilaisia vaihtoehtoja on
voidaan valita alkio kolmella tavalla. Näin jatkamalla havaitaan, että erilaisia vaihtoehtoja on 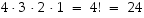 .
Siten erilaisia permutaatioita, joissa ykkönen kuvautuu itselleen, on ryhmässä
.
Siten erilaisia permutaatioita, joissa ykkönen kuvautuu itselleen, on ryhmässä 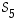 olemassa 24 erilaista.
olemassa 24 erilaista.
Huomautus.
P
ositiivisen kokonaisluvun
n−
kertoma
on 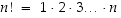 .
.
ii) Tarkastellaan sitten sellaisia permutaatioita, jotka kuvaavat joko alkiot 1 ja 2 molemmat itselleen tai molemmat toisikseen.
Ratkaisutapa I. Nyt joko sekä ykkönen että kakkonen kuvautuvat itselleen tai toisilleen. Näin ollen permutaatio voi olla kahta muotoa:
Tilanteet ovat identtisiä vaihtoehtojen määrän suhteen. Koska sekä vasemman, että oikeanpuoleinen voidaan muodostaa 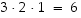 tavalla edellisen kohdan perustelun nojalla, on ehtojen mukaisia permutaatioita
tavalla edellisen kohdan perustelun nojalla, on ehtojen mukaisia permutaatioita 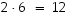 kappaletta.
kappaletta.
Ratkaisutapa II.
Koska alkiot 1 ja 2 kuvautuvat joko itselleen tai toisilleen, on vaihtoehtoja niiden järjestykselle 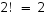 kpl. Jälkimmäisten kolmen järjestysmahdollisuuksia on
kpl. Jälkimmäisten kolmen järjestysmahdollisuuksia on 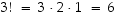 kpl. Yhteensä vaihtoehtoja siis
kpl. Yhteensä vaihtoehtoja siis 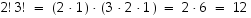 .
.
b) Pyritään nyt yleistämään
a)
-kohdan ensimmäisen alakohdan tilanne ryhmään 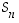 .
.
i) Koska oletuksen mukaan
k
ensimmäistä alkiota kuvautuvat itselleen, ei valinnan varaa näiden osalta permutaatiota muodostettaessa ole ja
k
:lle ensimmäiselle termille vaihtoehtoja on tasan yksi kullekin. Alkion 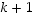 kuvautuminen voidaan valita
kuvautuminen voidaan valita 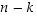 tavalla, alkion
tavalla, alkion 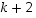 kuvautuminen voidaan valita
kuvautuminen voidaan valita 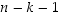 tavalla, jne. Näin ollen erilaisia, ehdot täyttäviä permutaatioita on
tavalla, jne. Näin ollen erilaisia, ehdot täyttäviä permutaatioita on 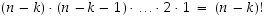 kappaletta.
kappaletta.
ii) Yleistämällä
a)
-kohdan toisen alakohdan ii) tilanne nähdään, että ensimmäisien
k
:n alkion kuvautumiset voidaan valita 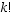 tavalla ja loppujen
tavalla ja loppujen 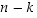 alkioiden kuvautuminen sen jälkeen
alkioiden kuvautuminen sen jälkeen 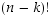 tavalla. Erilaisia annetut ehdot täyttäviä permutaatioita on siten
tavalla. Erilaisia annetut ehdot täyttäviä permutaatioita on siten 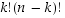 kappaletta.
kappaletta.
Esimerkki.
Havainnollistetaan edellistä kohtaa konkreetin esimerkin kautta. Valitaan 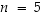 ja
ja 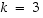 ,
jolloin saadaan seuraavat permutaatiomahdollisuudet:
,
jolloin saadaan seuraavat permutaatiomahdollisuudet:
Saatiin siis 6 erilaista vaihtoehtoa sille, miten kolme itselleen tai toisilleen kuvautuvaa alkiota voivat kuvauksessa kuvautua. Kussakin tapauksessa muuttujien 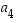 ja
ja 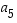 paikalle voidaan alkiot valita kahdella tavalla. Näin vaihtoehtoja tulee kaikkiaan
paikalle voidaan alkiot valita kahdella tavalla. Näin vaihtoehtoja tulee kaikkiaan 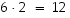 .
Tämä on yhtäpitävää aiemman kaavan kanssa tapauksessa
.
Tämä on yhtäpitävää aiemman kaavan kanssa tapauksessa 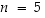 ja
ja 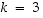 ,
sillä
,
sillä 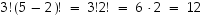 .
.