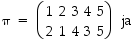
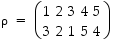
tulot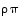 
ja 
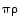sekä käänteispermutaatiot 
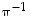ja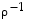 
.
Huomaa, että permutaatioryhmien alkioiden tulot ovat oikeasti yhdistettyjä kuvauksia, esim.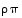 
tarkoittaa yhdistettyä kuvausta 
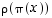; tässä tapauksessa 
.
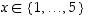Koska kyseessä on yhdistetty kuvaus, täytyy permutaatioiden "tulo" (jonka lopputulos on tyypiltään myöskin permutaatio) määrätä oikealta vasemmalle.
Annetaan nyt yhdistetylle kuvaukselle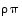 
ensin syöte 
,
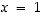jolloin
Ensin siis kuvaus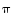 
kuvaa syötteen 1 arvoksi 2 ja tämän jälkeen kuvaus 
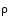kuvaa saamansa syötteen (luvun 2) luvuksi 2. Samaa ideaa syöteluvuille 
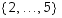toistamalla saadaan 
,
,
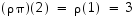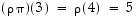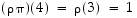ja 
.
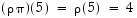Yhdistetty kuvaus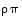 
on siten permutaatiomuodossa
Kuvausjärjestystä vaihtamalla saadaan toisinpäin yhdistetty kuvaus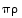 
:
Käänteispermutaation määrittäminen tapahtuu yksinkertaisesti permutaatioesityksen rivien vaihdolla, katso vinkkiä kurssikirjan s. 50. Alekkain sijoittuvat lukuparit voi lopuksi järjestää ylärivin mukaan kasvaviksi. Nyt siis
Käänteispermutaatiot ovat siten samoja kuin itse permutaatiot. Näin on vain sattumalta!
• Permutaatiot: http://en.wikipedia.org/wiki/Permutation
.
