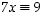renkaassa 
.
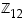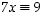renkaassa .
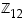Ratkaistavana on yhtälö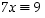 
renkaassa 
.
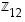Koska 
,
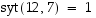on alkio 7 kääntyvä tässä renkaassa (kurssikirjan s. 41 Lause 4.1.) ja näin ollen yhtälölle on olemassa yksikäsitteinen ratkaisu.
Koska kurssikirjan s. 42 Lauseen 4.4. nojall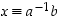a 
,
missä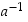 
on alkion 
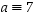käänteisalkio ja 
,
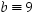täytyy ensin etsiä ensin alkion 7 käänteisalkio. Edellisen tehtävän 4.6 mukaan sen käänteisalkio on se itse; tämä pätee tosiaan, sillä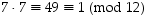 
.
Nyt
x
voidaan ratkaista lauseen 4.5. mukaan:
Tehtävän ratkaisu on siis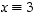 
.
Tarkistus: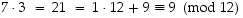 
.
Lisätietoja.
Huomaa, että ratkaisu on nimenomaan koko se ekvivalensiluokka, jonka yksi edustaja on alkio 3. Yleensä renkaassa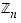 
ekvivalenssiluokan edustajaksi valitaan se luokan (yksikäsitteinen) jäsen
a,
jolle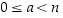 
.
Voitaisiin kuitenkin valita mikä tahansa kyseisen luokan, tässä tapauksessa luokan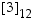 
,
edustaja muuttujaksi
x
ja edelleen pyydetty yhtälö toteutuisi.
Esimerkki.
Koska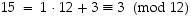 
,
voidaan valita ekvivalenssiluokan edustajaksi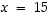 
,
jolloin 
,
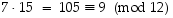sillä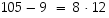 
.
Edelleen voitaisiin valita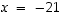 
,
jolloin 
,
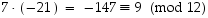sillä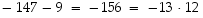 
.
.