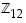 alkiot, joilla on käänteisalkio, ja ilmoita kunkin käänteisalkio.
alkiot, joilla on käänteisalkio, ja ilmoita kunkin käänteisalkio. 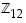 alkiot, joilla on käänteisalkio, ja ilmoita kunkin käänteisalkio.
alkiot, joilla on käänteisalkio, ja ilmoita kunkin käänteisalkio.
Kääntyviä alkioita voi etsiä joko kokeilemalla tai hyödyntämällä kurssikirjan s. 41 Lauseen 4.1. antamaa tietoa, jonka mukaan renkaan 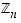 alkiolla
a
on käänteisalkio täsmälleen silloin, kun luvut
a
ja
n
ovat keskenään jaottomat eli
alkiolla
a
on käänteisalkio täsmälleen silloin, kun luvut
a
ja
n
ovat keskenään jaottomat eli 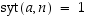 .
Hyödynnetään ko. lausetta. Koska
.
Hyödynnetään ko. lausetta. Koska 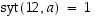 ja
ja 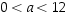 ,
kun
,
kun 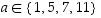 ,
niin renkaan
,
niin renkaan 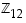 kääntyvät alkiot ovat 1, 5, 7 ja 11.
kääntyvät alkiot ovat 1, 5, 7 ja 11.
Ratkaisutapa I.
Modulin12 ollessa pieni voidaan alkioiden 1, 5, 7 ja 11 käänteisalkiot etsiä yksinkertaisesti kokeilemalla. Kullekin alkiolle
a
täytyy löytää joku renkaan alkio
b
siten, että tulo
ab
on 1 renkaassa 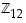 .
Alkio
b on silloin alkion a käänteisalkio.
Alkio 1 on aina oma käänteisalkionsa, sillä
.
Alkio
b on silloin alkion a käänteisalkio.
Alkio 1 on aina oma käänteisalkionsa, sillä 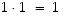 .
Etsitään loput käänteisalkiot:
.
Etsitään loput käänteisalkiot:
Kääntyvän alkion käänteisalkio on myös kääntyvä. Siis kääntyville alkioille 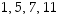 pätee, että niiden käänteisalkiot kuuluvat joukkoon
pätee, että niiden käänteisalkiot kuuluvat joukkoon 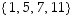 .
.
Luvun 5 käänteisalkio: Ensinnäkin 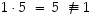 ,
joten alkio 1 ei ole alkion 5 käänteisalkio. Kokeilemalla seuraavalla mahdollisella alkiolla eli viitosella huomataan, että
,
joten alkio 1 ei ole alkion 5 käänteisalkio. Kokeilemalla seuraavalla mahdollisella alkiolla eli viitosella huomataan, että 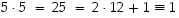 .
Tämän mukaan
.
Tämän mukaan 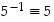 ,
joten myös alkio 5 on itse oma käänteisalkionsa.
,
joten myös alkio 5 on itse oma käänteisalkionsa.
Samaan tapaan jatkamalla havaitaan, että myös alkiot 7 ja 11 ovat omia käänteisalkioitaan: 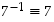 ja
ja 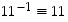 .
Näin on, sillä
.
Näin on, sillä 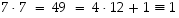 ja
ja 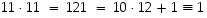 .
.
Huomautus.
Renkaissa 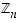 käytetään termin
luku
sijasta termiä
alkio.
käytetään termin
luku
sijasta termiä
alkio.
Ratkaisutapa II.
Jos kokeileminen ei syystä tai toisesta onnistu, voidaan kääntyvän alkion
a
käänteisalkio lauseen 4.1. avulla etsiä suurimman yhteisen tekijän 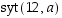 monikertasummaesityksen avulla. Tehdään näin alkioille 5 ja 7.
monikertasummaesityksen avulla. Tehdään näin alkioille 5 ja 7.
i) Luvulle
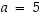 on
on 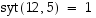 .
Eukleideen algoritmilla saadaan
.
Eukleideen algoritmilla saadaan
Paluualgoritmia käyttämällä saadaan suurin yhteinen tekijä 1 esitettyä lukujen 12 ja 5 monikertasummana:
Näin ollen alkion
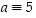 käänteisalkio on
käänteisalkio on 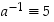 .
.
joten paluualgoritmia käyttämällä saadaan syt esitettyä lukujen 12 ja 7 monikertasummana:
Tämän mukaan −5 on alkion 7 käänteisalkio. Koska 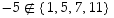 ,
tulee valita jokin toinen edustaja käänteisalkiota vastaavasta ekvivalenssiluokasta (ks. kurssikirjan s. 35). Koska
,
tulee valita jokin toinen edustaja käänteisalkiota vastaavasta ekvivalenssiluokasta (ks. kurssikirjan s. 35). Koska 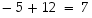 ,
valitaan edustajaksi luku 7. Täten siis alkio 7 on itsensä käänteisalkio.
,
valitaan edustajaksi luku 7. Täten siis alkio 7 on itsensä käänteisalkio.
Huomautus. Joskus tämä paluualgoritmista saatava kerroin voi olla negatiivinen, kuten edellä alkion 7 käänteisalkiota etsittäessä käy. Tämä ei kuitenkaan haittaa, sillä kyseiset ratkaisut kuuluvat kuitenkin samaan jäännösluokkaan (ekvivalenssiluokkaan, ks. kurssikirjan s. 35) ja näin käänteisalkioksi voidaan valita mikä tahansa edustaja kyseisestä jäännösluokasta.
Tässä tehtävässä kukin kääntyvä alkio on oma käänteisalkionsa. Huomaa, että tämä on sattuma eikä näin suinkaan käy aina.
Kääntyvät alkiot ja niiden käänteisalkiot kuvana:
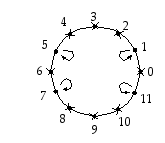
Lisätietoja.
Käänteisalkioita tarvitsee itseasiassa etsiä vain renkaan puolikkaasta, sillä toinen puoli menee symmetrian mukaan käyttämällä merkin vaihtoa apuna. Esimerkiksi edellä 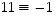 ja
ja 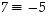 ,
joten
,
joten 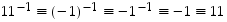 ja
ja 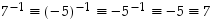 .
.