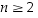 ei ole alkuluku, niin sillä on tekijänä jokin alkuluku
ei ole alkuluku, niin sillä on tekijänä jokin alkuluku 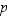 ,
jolle
,
jolle 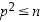 .
.
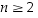 ei ole alkuluku, niin sillä on tekijänä jokin alkuluku
ei ole alkuluku, niin sillä on tekijänä jokin alkuluku 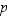 ,
jolle
,
jolle 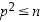 .
.
Ratkaisutapa I.
Kun
n
ei ole alkuluku, on se yhdistetty luku ja tällöin olemassa sellaiset kokonaisluvut
r
ja
s,
että 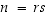 ja
ja 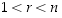 (jolloin myös
(jolloin myös 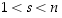 ). Voidaan olettaa, että
r
on pienempi tai yhtä suuri kuin
s,
ts.
). Voidaan olettaa, että
r
on pienempi tai yhtä suuri kuin
s,
ts. 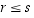 .
Luku
r
on joko itse alkuluku tai sillä on pienempi alkutekijä. Valitaan tämä alkuluku tai alkutekijä luvuksi
p.
Nyt
.
Luku
r
on joko itse alkuluku tai sillä on pienempi alkutekijä. Valitaan tämä alkuluku tai alkutekijä luvuksi
p.
Nyt 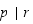 ja
ja 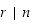 ,
joten myös
,
joten myös 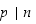 .
Koska joko
.
Koska joko 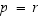 tai
tai 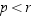 ,
niin
,
niin 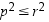 .
Toisaalta
.
Toisaalta 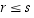 ,
joten
,
joten 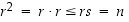 .
Näin on saatu että
.
Näin on saatu että 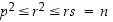 .
.
Ratkaisutapa II. Aritmetiikan peruslauseen (4.4.) nojalla yhdistetylle luvulle n on olemassa esitys alkulukujen tulona:
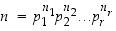 ,
missä
,
missä 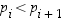 kaikilla indekseillä
i
(
kaikilla indekseillä
i
(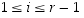 ).
).
Koska
n
ei ole alkuluku, on sen alkutekijäesityksessä oltava vähintään kaksi alkulukua (eri suurta tai yhtä suurta). Merkitään 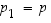 ja
ja 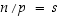 .
Nyt
.
Nyt 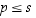 ,
sillä
s
sisältää vähintään yhden alkutekijän, joka on suurempi tai yhtä suuri kuin luku
p.
Lisäksi
,
sillä
s
sisältää vähintään yhden alkutekijän, joka on suurempi tai yhtä suuri kuin luku
p.
Lisäksi 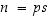 ,
joten
,
joten 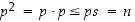 ,
mikä todistaa väitteen.
,
mikä todistaa väitteen.