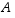 ,
,
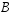 ja
ja 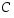 saman perusjoukon
saman perusjoukon 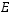 osajoukkoja. Osoita oikeaksi ns. osittelulaki
osajoukkoja. Osoita oikeaksi ns. osittelulaki 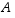 ,
,
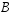 ja
ja 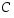 saman perusjoukon
saman perusjoukon 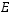 osajoukkoja. Osoita oikeaksi ns. osittelulaki
osajoukkoja. Osoita oikeaksi ns. osittelulaki
Ratkaisutapa I.
Osoitetaan väite todeksi Vennin kuvion avulla. Kuvassa vasemmalla on 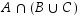 ,
oikealla
,
oikealla 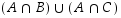 .
.
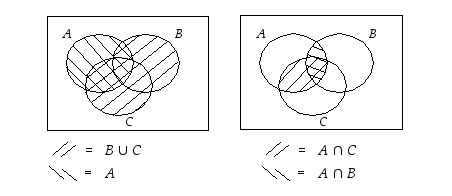
Vasemman kuvion tuplaviivoitettu alue 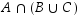 ja oikean puolen viivoitettu alue
ja oikean puolen viivoitettu alue 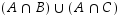 ovat samat kuten väitettiinkin.
ovat samat kuten väitettiinkin.
• Venn diagrams: http://en.wikipedia.org/wiki/Venn_diagram
Ratkaisutapa II.
Joukko-opillinen todistus tehdään seuraavasti. Todistuksen merkintöjen lyhentämiseksi merkitään 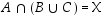 ja
ja 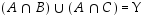 .
Väite on, että
.
Väite on, että 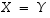 .
Todistetaan se kahdessa osassa osoittamalla, että kyseiset joukot ovat toistensa osajoukkoja eli että mikä tahansa alkio, joka kuuluu yhteen näistä joukoista, kuuluu myös toiseen.
.
Todistetaan se kahdessa osassa osoittamalla, että kyseiset joukot ovat toistensa osajoukkoja eli että mikä tahansa alkio, joka kuuluu yhteen näistä joukoista, kuuluu myös toiseen.
Osoitetaan ensin, että 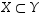 .
Olkoon
.
Olkoon 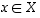 mielivaltainen. Täytyy osoittaa, että
mielivaltainen. Täytyy osoittaa, että 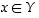 .
Koska
.
Koska 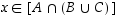 ,
seuraa tästä, että
,
seuraa tästä, että 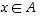 ja
ja 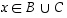 .
Edelleen pätee, että
.
Edelleen pätee, että 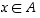 ja lisäksi
ja lisäksi 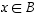 tai
tai 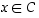 .
Nyt edellisen nojalla joko
.
Nyt edellisen nojalla joko 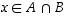 tai
tai 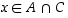 ,
joten
,
joten 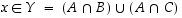 .
.
Osoitetaan sitten, että 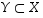 .
Olkoon
.
Olkoon 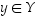 mielivaltainen. Täytyy osoittaa, että
mielivaltainen. Täytyy osoittaa, että 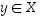 .
Koska
.
Koska 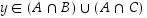 ,
seuraa tästä että
,
seuraa tästä että 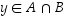 tai
tai 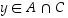 .
Näin ollen pätee varmasti, että
.
Näin ollen pätee varmasti, että 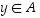 ja lisäksi
ja lisäksi 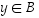 tai
tai 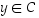 ,
joten
,
joten 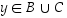 ja edelleen
ja edelleen 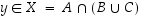 .
.
Koska nyt on osoitettu, että 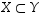 ja
ja 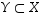 ,
seuraa tästä, että
,
seuraa tästä, että 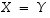 eli
eli 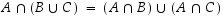 .
.