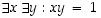Tehtävä 1.4. Seuraavissa väitteissä kaikki muuttujat voivat olla nollasta eroavia kokonaislukuja. Määrää kunkin väitelauseen totuusarvo. Jos se on mielestäsi epätosi, niin muodosta myös lauseen negaatio.

a) ,

b) ,

c) .

Ratkaisu

a) Väite on tosi, sillä on olemassa nollasta eroavat kokonaisluvut x ja y siten, että niiden tulo on 1: jos nimittäin valitaan esimerkiksi luvut 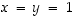, niin tällöin 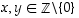ja .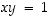

b) Kun ehto 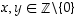otetaan huomioon, luetaan väite 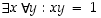seuraavasti: On olemassa sellainen nollasta eroava kokonaisluku x, että kaikilla nollasta eroavilla kokonaisluvuilla y tulo 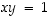. Väite on ilmeisen epätosi, sillä jotta väite pätisi, olisi jollekin x oltava 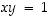kaikilla muuttujan y arvoilla eli lausekkeen 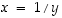on oltava vakio, mitä se ei tietenkään ole.

Väitteen negaatio on

Se on tosi, sillä valitsemalla esimerkiksi 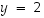saadaan 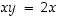, mikä on aina parillinen eikä siten voi olla 1 millään nollasta eroavalla kokonaisluvulla x.

Huomautus. Tässä sama muuttujan y arvo, esim. 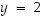, kelpaa ehtojen mukaiseksi luvuksi kaikille 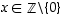. Voisi kuitenkin aivan hyvin olla niin, että jokaiselle x olisi oma (mahdollisesti erisuuri) y. Oleellista on vain se, että jokaiselle x on olemassa sopiva y.

c) Väite näyttää taaskin olevan epätosi, joten osoitetaan se sellaiseksi. Jos väitteen negaatio voidaan osoittaa todeksi, on alkuperäisen väitteen oltava epätosi, sillä väitteellä ja sen negaatiolla ei logiikan sääntöjen mukaan voi olla sama totuusarvo.

Väitteen negaatio on 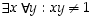. Jos tässä valitaan esimerkiksi 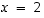, niin tällöin 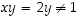kaikilla 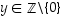. Negaatio on siten tosi ja alkuperäinen väite on epätosi.

[Opiskelutehtäviä 1]