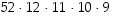kappaletta. Kaikkia mahdollisuuksia on seuraavasti: ensimmäisellä kortilla nostovaihtoehtoja on 52, sitten 51 jne. ja viidennellä nostolla 48. Kaikki mahdollisuuksia on siis 
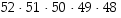kappaletta. Kysytty todennäköisyys on näin ollen
Ratkaisutapa I.
Ensimmäiseksi kortiksi käyvät kaikki kortit, mahdollisuuksia on siis 52. Seuraavalle kortille suotuisia mahdollisuuksia on ensimmäisenä nostetun kortin kanssa samaa maata olevat kortit, yhteensä 12 korttia. Kolmannella nostolla vaihtoehtoja on 11, sitten 10 ja lopuksi viidennellä nostolla 9. Suotuisia tapauksia on siis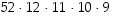
kappaletta. Kaikkia mahdollisuuksia on seuraavasti: ensimmäisellä kortilla nostovaihtoehtoja on 52, sitten 51 jne. ja viidennellä nostolla 48. Kaikki mahdollisuuksia on siis
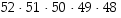kappaletta. Kysytty todennäköisyys on näin ollen
Ratkaisutapa II.
Esimerkiksi padoille: viisi pataa voidaan nostaa pakasta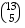 
eri tavalla (kunkin eri maan kortteja on korttipakassa 13 kpl). Viisi korttia voidaan nostaa korttipakasta 
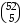eri tavalla. Todennäköisyys, että viidellä nostolla kaikki kortit ovat patoja kun kortteja ei nostojen välillä palauteta pakkaan, on suotuisat jaettuna kaikilla tapauksilla: 
.
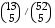Koska eri maita on neljä, saadaan lopulta kysytty todennäköisyys (ks. kurssikirjan s. 90, Otanta ilman takaisinpanoa):
Ratkaisutapa III. Lasketaan todennäköisyyksien tulo
Tässä ratkaisutavassa tosin käytetään ehdollisen todennäköisyyden käsitettä ja todennäköisyyksien kertolaskusääntöä, jota ei ole vielä tähän mennessä käsitelty.
