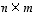olevan matriisin 
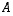transponoitu
matriisi eli sen
transpoosi on 
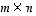-matriisi 
,
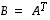jolle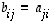 
kaikille indekseille 
.
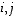Muita käytettyjä merkintöjä ovat mm. 
,
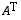
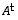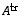ja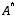 
.
Neliömäinen matriisitaulukko on helppo ajatella peilatuksi esimerkiksi lävistäjänsä suhteen. Yleisesti tyyppiä 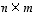olevan matriisin
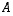transponoitu
matriisi eli sen
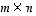transpoosi on -matriisi ,
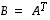jolle 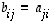kaikille indekseille .
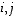Muita käytettyjä merkintöjä ovat mm. ,
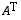
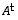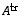ja .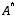
Mutta mitä tällä transponoinnilla on tekemistä lineaarikuvausten kanssa? Tähän ei vielä pystytä vastaamaan. Myöhemmin tähän vastataan - ainakin osittain - tämän luvun lopussa ortogonaalisen matriisin yhteydessä lauseessa 8.17 sekä symmetrisen matriisin ominaisarvoprobleeman yhteydessä luvussa 11 (pykälässä Symmetrisen matriisin tilanne).
Neliömatriisia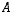 
sanotaan kuvaavasti
symmetriseksi, mikäli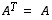 
.
Symmetrisen matriisin lävistäjäalkiot saavat olla mitä tahansa, mutta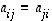 
aina kun 
.
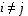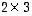-matriisin transpoosi on tyyppiä 
.
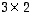Esimerkiksi
on symmetrinen täsmälleen silloin, kun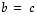 
.
Seuraavassa on eräitä laskusääntöjä transpoosin muodostamiselle.
Kun alla esiintyvien matriisien tyypit ovat lausekkeiden muodostamisen kannalta keskenään yhteensopivat (eri kohdissa ehdot voivat olla erilaiset), pätevät seuraavat säännöt.
(e) jos lisäksi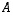 
on (neliömatriisi ja) kääntyvä, myös 
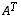on kääntyvä ja erityisesti 
.
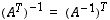Todistus. Osoitetaan vain kohdat (d) ja (e) oikeiksi. Muut kohdat ovat ilmeisiä tai varsin helposti todennettavia.
(d) Olkoon matriisi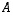 
tyyppiä 
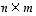ja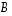 
tyyppiä 
.
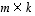Silloin tulomatriisi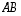 
on määritelty, on tyyppiä 
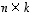ja sen alkio paikassa 
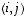on
Matriisi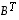 
on taas tyyppiä 
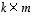ja matriisi 
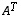tyyppiä 
.
Tulomatriisi 
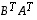on siten myös määritelty, on tyyppiä 
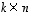ja sen alkio paikassa 
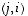on
Se on siis sama kuin matriisin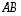 
alkio paikassa 
.
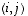Siten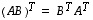 
.
Huomaa tässä säännössä kertomisjärjestyksen muuttuminen!
(e) Edellisen kohdan perusteella on
mikä todistaakin väitteen. (Matriisin todistamisesta käänteismatriisiksi katso lauseen 8.10 todistuksen alkua.)
.
-matriisi 
,
,
(kaikille 
), 
,
.
,
