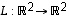 tason lineaarikuvaus, jolle
tason lineaarikuvaus, jolle
Tarkastellaan ensin johdatteluna yksinkertaista esimerkkiä. Olkoon 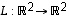 tason lineaarikuvaus, jolle
tason lineaarikuvaus, jolle
Yleisesti se kuvaa vektorin 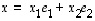 seuraavasti:
seuraavasti:
Kun merkitään, että 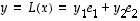 ,
saadaan ehdot
,
saadaan ehdot
Kirjoitetaan tämä 'muodollisesti'
on ns. 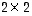 -
matriisi ja oikeanpuoleinen tulo lasketaan auki 'kertomalla rivillä sarake'.
-
matriisi ja oikeanpuoleinen tulo lasketaan auki 'kertomalla rivillä sarake'.
Tässä siis matriisi on sellainen taulukko, jossa lineaarikuvauksen määräämät kertoimet ovat sillä tavalla taulukoituina, että
· ensimmäinen sarake 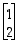 muodostuu vektorin
muodostuu vektorin 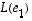 koordinaateista ja
koordinaateista ja
· toinen sarake 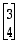 muodostuu vektorin
muodostuu vektorin 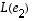 koordinaateista.
koordinaateista.
Lisäksi yhtälössä esiintyy yksisarakkeisia matriiseja, joista
· matriisi  muodostuu vektorin
muodostuu vektorin 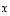 koordinaateista ja
koordinaateista ja
· matriisi  muodostuu vektorin
muodostuu vektorin 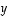 koordinaateista.
koordinaateista.
Tehdään tämän jälkeen yleistys mielivaltaiselle lineaarikuvaukselle 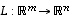 .
.
Olkoon 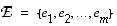 jokin avaruuden
jokin avaruuden 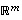 kanta ja
kanta ja 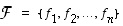 jokin avaruuden
jokin avaruuden 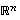 kanta sekä olkoot kuvavektorien
kanta sekä olkoot kuvavektorien 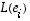 koordinaattiesitykset seuraavat:
koordinaattiesitykset seuraavat:
Sama voidaan lausua summausmerkkiä ja -indeksiä käyttäen seuraavasti
Silloin mielivaltaisen vektorin 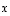 kuvaksi saadaan
kuvaksi saadaan
Tässä esiintyvistä kertoimista voidaan muodostaa taulukko
Tätä taulukkoa sanotaan
tyyppiä 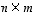 olevaksi
matriisiksi tai
olevaksi
matriisiksi tai 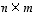 -
matriisiksi, jossa on siis
-
matriisiksi, jossa on siis 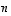 riviä ja
riviä ja 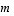 saraketta. Yleisiä
indeksejä käyttäen lyhennetään taulukko muotoon
saraketta. Yleisiä
indeksejä käyttäen lyhennetään taulukko muotoon 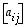 ,
missä ensimmäinen indeksi
,
missä ensimmäinen indeksi 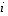 ilmaisee rivinumeron ja toinen indeksi
ilmaisee rivinumeron ja toinen indeksi 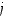 sarakenumeron muuttumisen.
sarakenumeron muuttumisen.
Lineaarikuvaukseen 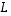 liitetään siis eräistä koordinaateista muodostettu matriisi
liitetään siis eräistä koordinaateista muodostettu matriisi 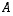 .
Yllä oleva päättely voidaan tehdä myös kääntäen: luvuista muodostuvasta matriisista
.
Yllä oleva päättely voidaan tehdä myös kääntäen: luvuista muodostuvasta matriisista 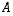 lähtien voidaan määritellä yllä esitettyyn tapaan yksikäsitteisesti lineaarikuvaus
lähtien voidaan määritellä yllä esitettyyn tapaan yksikäsitteisesti lineaarikuvaus 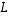 .
Lineaarikuvaukset ja matriisit vastaavat siten yksikäsitteisesti toisiaan. Tämä pitää tosin paikkansa vain niin kauan kuin vastaavuudessa käytetyt kannat pidetään samoina. Ellei muuta mainita, käytetään kantoina luonnollisia kantoja. Kantojen vaihdon vaikutuksia tähän vastaavuuteen selvitetään luvussa 9.
.
Lineaarikuvaukset ja matriisit vastaavat siten yksikäsitteisesti toisiaan. Tämä pitää tosin paikkansa vain niin kauan kuin vastaavuudessa käytetyt kannat pidetään samoina. Ellei muuta mainita, käytetään kantoina luonnollisia kantoja. Kantojen vaihdon vaikutuksia tähän vastaavuuteen selvitetään luvussa 9.
eli sama taas muodollisesti lausuttuna
Yllä muodostettu taulukko 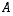 on lineaarikuvausta
on lineaarikuvausta 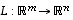 kannoissa
kannoissa 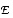 ja
ja 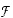 vastaava
matriisi. Samalla tulee määriteltyä se, mitä tarkoitetaan matriisin ja vektorin
tulolla. Merkitään matriisin riippuvuus lineaarikuvauksesta näkyviin seuraavasti
vastaava
matriisi. Samalla tulee määriteltyä se, mitä tarkoitetaan matriisin ja vektorin
tulolla. Merkitään matriisin riippuvuus lineaarikuvauksesta näkyviin seuraavasti
(tai tarvittaessa tarkemmin 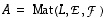 ,
mikäli kantariippuvuudet halutaan jostain syystä tuoda esiin). Matriisi
,
mikäli kantariippuvuudet halutaan jostain syystä tuoda esiin). Matriisi 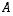 muodostetaan siis sijoittamalla kantavektoreiden
muodostetaan siis sijoittamalla kantavektoreiden 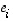 kuvien
kuvien 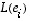 koordinaatit sen sarakkeiksi:
koordinaatit sen sarakkeiksi:
Kaiken kaikkiaan on saatu seuraavat tulokset:
(a) Jokaista lineaarikuvausta vastaa yksi matriisi - ja kääntäen.
(b) Lineaarikuvauksen lausekkeet (yllä 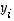 ) ovat muuttujien (yllä
) ovat muuttujien (yllä 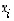 ) muodollisia lineaarikombinaatioita. Kääntäen tällä tavalla saadaan aina lineaarikuvaus määriteltyä.
) muodollisia lineaarikombinaatioita. Kääntäen tällä tavalla saadaan aina lineaarikuvaus määriteltyä.
(c) Lineaarisesta yhtälöryhmästä voidaan muodostaa yllä olevan mukaisesti matriisiesitys ja siitä edelleen lineaarikuvaus. Lineaarikuvaus, matriisi ja yhtälöryhmä ovat siis saman asian eri ilmentymiä.
(a) Kuvaus 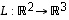 ,
jolle
,
jolle  ,
on lineaarinen jo sillä perusteella, että lausekkeet
,
on lineaarinen jo sillä perusteella, että lausekkeet 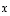 ,
,
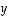 ja
ja 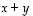 ovat muuttujien
ovat muuttujien 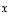 ja
ja 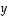 lineaarikombinaatioita. Tälle kuvaukselle
lineaarikombinaatioita. Tälle kuvaukselle 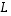 on
on
joten sitä vastaa (luonnollisissa kannoissa) 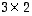 -matriisi
-matriisi
(b) Myös kuvaus 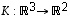 ,
jolle
,
jolle 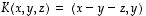 ,
on lausekkeiden lineaarisuuden perusteella lineaarinen ja sille
,
on lausekkeiden lineaarisuuden perusteella lineaarinen ja sille
Opiskelutehtävässä 16 todettiin, että 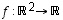 ,
,
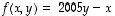 on lineaarinen. Miten voisit nähdä lineaarisuuden nopeammin?
on lineaarinen. Miten voisit nähdä lineaarisuuden nopeammin?
Jatkossa samastetaan usein vektori 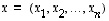 ja sen komponenteista muodostettu yksisarakkeinen matriisi:
ja sen komponenteista muodostettu yksisarakkeinen matriisi:
Tällöin voidaan kirjoittaa, että 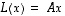 ,
kun
,
kun 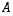 on lineaarikuvausta
on lineaarikuvausta 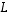 vastaava matriisi. Samoin voidaan tulossa
vastaava matriisi. Samoin voidaan tulossa 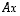 puhua matriisin kohdistamisesta tai soveltamisesta vektoriin
puhua matriisin kohdistamisesta tai soveltamisesta vektoriin 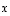 aivan kuin kuvauksillekin. Huomaa, että mikäli tällaisissa tilanteissa matriisilla kertominen kohdistuu yhtä muuttujaa isompaan lausekkeeseen, sarakevektorin ympärillä joudutaan käyttämään sulkeita. Esimerkiksi lausekkeessa
aivan kuin kuvauksillekin. Huomaa, että mikäli tällaisissa tilanteissa matriisilla kertominen kohdistuu yhtä muuttujaa isompaan lausekkeeseen, sarakevektorin ympärillä joudutaan käyttämään sulkeita. Esimerkiksi lausekkeessa 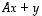 matriisilla kertominen kohdistuu vain vektoriin
matriisilla kertominen kohdistuu vain vektoriin 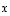 ,
mutta merkinnässä
,
mutta merkinnässä 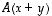 se kohdistuu vektorisummaan
se kohdistuu vektorisummaan 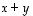 .
.
Edellä olevassa esimerkissä 7.2 voidaan saatujen matriisien avulla muodostaa (tarkistuksen vuoksi) lineaarikuvauksen lausekkeet seuraavasti:
Tason lineaarikuvaukselle 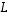 olkoot
olkoot 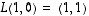 ja
ja 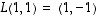 .
Määrää kuvauksen
.
Määrää kuvauksen 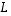 lauseke a) lineaarisuussääntöjen, b) matriisin avulla
lauseke a) lineaarisuussääntöjen, b) matriisin avulla
Määrää tason (a) peilausta pystyakselin suhteen ja (b) 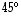 kiertoa vastaavat matriisit
kiertoa vastaavat matriisit
vastaavan lineaarikuvauksen lauseke. Selitä geometrisesti, mitä kuvaus tekee (piirrä avuksi jonkin kuvan muuntuminen).