Lineaarisen kuvauksen mieltämiseksi tarkastellaan ensin geometrisesti kolmea tason muunnosta:
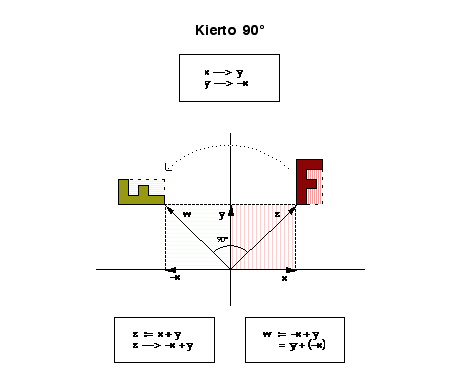
· 90 asteen kiertoa origon suhteen vastapäivään,
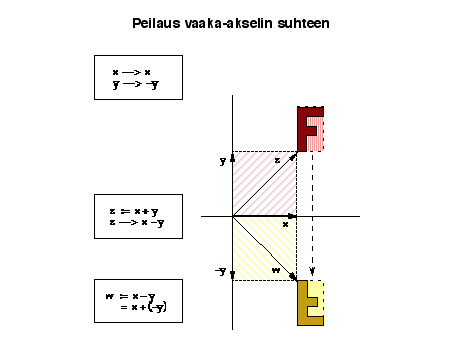
· peilausta vaaka-akselin suhteen sekä
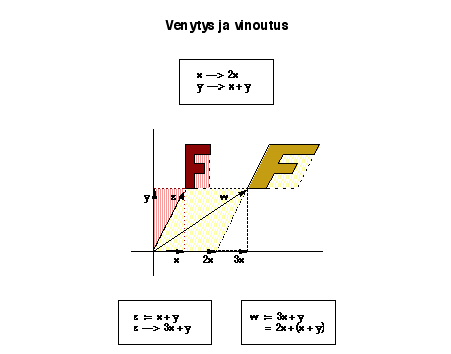
· (erästä) venytystä ja vinoutusta.
Tarkastelemalla alla olevia kuvia voi huomata, että jokaisessa näistä muunnoksista F -kirjaimen muotoinen kuvio säilyy suoraviivaisena, mahdollisesti vain sen asema muuttuu ja se venyttyy muodoltaan. Erityisesti kaikissa tapauksissa kaksinkertaiset vektorit kuvautuvat kaksinkertaisiksi, kolminkertaiset kolminkertaisiksi jne. Samoin voi kussakin esimerkissä vakuuttua siitä, että minkä tahansa kahden vektorin summavektorin kuva on aina sama kuin näiden vektorien kuvavektorien summa. Tämän tapaisia muunnoksia tarkastellaankin lähemmin jatkossa.
Yleisesti määritellään, että kuvaus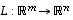 
on
lineaarinen eli se on
lineaarikuvaus, jos kaikilla vektoreilla 
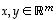ja kaikilla luvuilla 
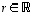on
Usein lineaarikuvauksien merkkinä käytetään isoja kirjaimia ja silloin voidaan argumenttien ympäriltä jopa jättää sulut pois, mikäli ne eivät muuten ole tarpeen. Lauseketta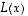 
merkitään silloin lyhyemmin 
.
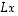Tässä kirjassa käytetään kuitenkin selvyyden vuoksi aina sulkeita. Huomaa, että merkintätavasta riippumatta esimerkiksi lausekkeesta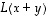 
ei saa sulkuja jättää pois, jotta se erottuisi lausekkeesta 
.
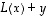Todetaan kolmen edellä olleen tasoesimerkin kuvausten lineaarisuudet.
Tason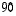 
asteen kierrossa vastapäivään muunnoskuvaus on sellainen kuvaus 
,
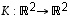jolle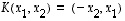 
.
Se on geometrisesti ajatellen selvästi lineaarinen. Todennetaan se vielä laskemallakin.
Peilauksessa vaaka-akselin suhteen muunnoskuvauksena on se kuvaus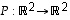 
,
jolle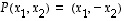 
.
Sekin on selvästi lineaarinen. Sen todentaminen onnistuu samaan tapaan kuin edellisessä esimerkissä ja jätetään lukijalle harjoittelutehtäväksi.
Venytys ja vinoutus -esimerkissä venytys muodostuu - kun sovitaan, että edellä olevassa kuvassa pystyvektori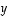 
on pituudeltaan kaksinkertainen vaakavektoriin 
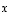verrattuna - kuvauksesta 
,
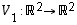jolle
ja (sen jälkeinen) vinoutus vuorostaan kuvauksesta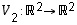 
,
jolle
Yhdistämällä nämä saadaan venytykseksi ja vinoutukseksi kuvaus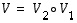 
,
jolle näin ollen
Todetaan tämän kuvauksen lineaarisuus. Ensinnäkin vektoreille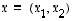 
ja 
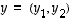on
Toiseksi vektorille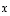 
ja luvulle 
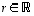on
On helppo todeta, että myös rakennusosina käytetyt kuvaukset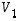 
ja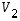 
ovat lineaarisia.
Jos kuvaus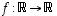 
on lineaarinen, silloin
ja siten luvulle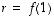 
on aina 
.
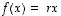Suoran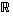 
lineaarikuvaukset ovat vain siis lukujen kertomisia jollain kiinteällä luvulla. Ne eivät siis siinä mielessä ole kovinkaan mielenkiintoisia!
Kuvaus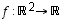 
,
,
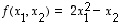ei ole lineaarinen, sillä esimerkiksi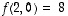 
,
mutta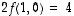 
.
Huomaa, että lineaarisuuden kumoamiseen riittää yksi konkreetti tilanne. Tässä syynä lineaarisuuden kumoutumiseen on olennaisesti neliöön korottaminen. Seuraavassa luvussa tullaan tarkemmin näkemään, minkä muotoisia lineaarikuvausten lausekkeet voivat olla (ks. lause 7.1).
Ovatko seuraavat kuvaukset lineaarisia?
Suoraan lineaarisuuden määrittelystä voidaan todentaa seuraavat tulokset.
Todistus.
Ensinnäkin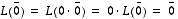 
,
missä nollavektoria on merkitty symbolilla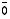 
erotukseksi luvusta 
.
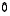Toiseksi
Jos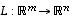 
on lineaarikuvaus ja vektorijoukko 
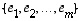on avaruuden 
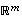kanta, kuvaus 
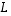määräytyy täysin kantavektorien kuvavektoreilla 
,
,
..., 
.
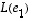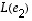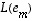Todistus.
Jokaisella vektorilla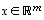 
on jokin koordinaattiesitys
Tällöin edellisen tuloksen mukaan
Lineaarikuvauksesta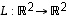 
tiedetään vain, että 
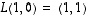ja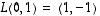 
.
(a) Määrä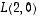ä 
ja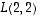 
- sekä graafisesti että laskien.
(c) Määrää yleisesti lauseke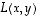 
.
(d) Kuvaa piirtämällä jonkin kuvion kuvautumista kuvauksessa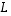 
.
Määrää tason (a) peilauksen pystyakselin suhteen, (b)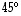 
kierron ja (c) 
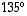kierron (vastapäivään) yleinen lauseke.
Geometrisesti tuntuu uskottavalta, että jos kaksi kuvausta säilyttävät suoraviivaisuuden, myös niiden yhdistetyllä kuvauksella on sama ominaisuus. Todetaan tämä mielikuva oikeaksi.
Jos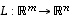 
ja 
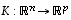ovat lineaarikuvauksia, myös kuvaus 
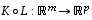on lineaarinen.
Todistus. Todetaan, että yhdistetylle kuvaukselle summa ja monikerta kuvautuvat oikein:
Esimerkissä 6.4 todettiin kuvausten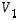 
ja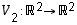 
yhdistetty kuvaus 
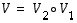lineaariseksi. Nyt voidaan lauseen 6.9 nojalla lyhyemmin todeta, että koska kuvaukset 
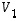ja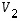 
ovat lineaarisia, myös yhdistetty kuvaus 
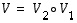on lineaarinen.
Kun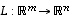 
on lineaarikuvaus, sen
monikerta (eli tarkemmin sanottuna luvulla kerrottu kuvaus)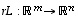 
määritellään luontevasti asettamalla kaikilla vektoreilla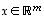 
Olkoon sitten kuvauksen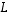 
lisäksi 
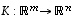(samojen avaruuksien välinen) lineaarikuvaus. Kuvausten 
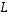ja 
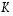summa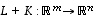 
määritellään yhtä luontevasti asettamalla kaikilla vektoreilla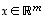 
Näin määritellyt kuvaukset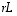 
ja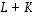 
osoittautuvat edelleen lineaarisiksi.
Jos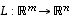 
ja 
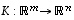ovat lineaarikuvauksia, myös summakuvaus 
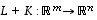on lineaarinen. Samoin monikertakuvaus 
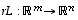on lineaarinen kaikilla luvuilla 
.
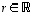Todistus. Todetaan, että summakuvauksessa vektorien summat ja monikerrat kuvautuvat oikein:
Vastaavasti sama voidaan todeta monikertakuvaukselle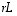 
.
Jätetään se harjoittelutehtäväksi.
Osoita, että kuvaukset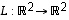 
,
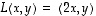ja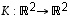 
,
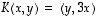ovat lineaarisia. Määritä summakuvaus 
,
,
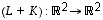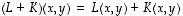ja totea myös sen lineaarisuus.
ja 
.
ja 
ovat tason vektoreita (pisteitä), niin 
,
niin 
.
on siten lineaarinen. 
,
.
.
.
,
,
,
.
on 
,
ja yleisemmin 
.
.
.
,
.
ja 
.
.
on lineaarinen. 
( 
). 
.
