Lineaarinen riippuvuus
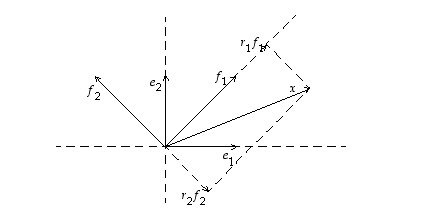
Aloitetaan tasoesimerkillä. Tason luonnollisen kannan vektoreilla 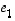 ja
ja 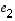 on todettu olevan sellainen erityinen ominaisuus, että mikä tahansa tason vektori voidaan yksikäsitteisesti esittää näiden lineaarikombinaationa. Tasossa on kuitenkin muitakin vektoreita, joilla on samanlainen 'kantaominaisuus´. Esimerkiksi, jos
on todettu olevan sellainen erityinen ominaisuus, että mikä tahansa tason vektori voidaan yksikäsitteisesti esittää näiden lineaarikombinaationa. Tasossa on kuitenkin muitakin vektoreita, joilla on samanlainen 'kantaominaisuus´. Esimerkiksi, jos 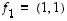 ja
ja 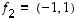 ,
jokaisella vektorilla
,
jokaisella vektorilla 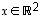 on mitä ilmeisimmin jokin esitys
on mitä ilmeisimmin jokin esitys 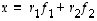 .
Itse asiassa tämä voidaan varmentaa laskemalla: jos
.
Itse asiassa tämä voidaan varmentaa laskemalla: jos 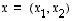 ,
valitsemalla
,
valitsemalla 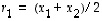 ja
ja 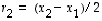 saadaan yhtälö
saadaan yhtälö 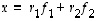 toteutumaan. Nämä kertoimet ovat kaiken lisäksi ainoat mahdolliset. Geometrisesti tämäkin on varsin selvää ja se voidaan toisaalta myös todentaa ratkaisemalla kertoimet yhtälöstä
toteutumaan. Nämä kertoimet ovat kaiken lisäksi ainoat mahdolliset. Geometrisesti tämäkin on varsin selvää ja se voidaan toisaalta myös todentaa ratkaisemalla kertoimet yhtälöstä 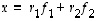 (missä vektorien
(missä vektorien 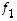 ja
ja 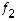 paikoille on ensin sijoitettu annetut lukuparit).
paikoille on ensin sijoitettu annetut lukuparit).
Millaiset vektorit sitten tällaisiksi 'kantavektoreiksi' kelpaavat? Jos vaikkapa olisi valittu vektorit 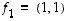 ja
ja 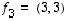 ,
tämä ei varmaankaan olisi käynyt! (Miksi?) Jos taas olisi valittu vektorit
,
tämä ei varmaankaan olisi käynyt! (Miksi?) Jos taas olisi valittu vektorit 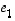 ,
,
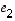 ja
ja 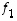 ,
kaikki tason vektorit voitaisiin kyllä ilmoittaa näiden lineaarikombinaationa valitsemalla yksinkertaisesti vektorin
,
kaikki tason vektorit voitaisiin kyllä ilmoittaa näiden lineaarikombinaationa valitsemalla yksinkertaisesti vektorin 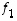 kertoimeksi aina nolla, mutta tämä esitystapa ei enää olisi suinkaan ainoa mahdollinen. Viimeksi mainittu vektori
kertoimeksi aina nolla, mutta tämä esitystapa ei enää olisi suinkaan ainoa mahdollinen. Viimeksi mainittu vektori 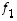 olisi siten tavallaan turha.
olisi siten tavallaan turha.
Tarkastellaan edellä kuvattua kantaominaisuutta yleisessä avaruudessa 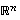 .
Siihen tarvitaan paria määrittelyä. Vektorin
.
Siihen tarvitaan paria määrittelyä. Vektorin 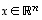 sanotaan olevan vektoreiden
sanotaan olevan vektoreiden 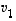 ,
,
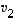 ,
...,
,
..., 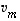 lineaarikombinaatio (tai
lineaariyhdistelmä), jos se voidaan esittää muodossa
lineaarikombinaatio (tai
lineaariyhdistelmä), jos se voidaan esittää muodossa
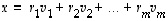
joillakin kertoimilla 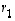 ,
,
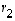 ,
...,
,
..., 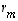 .
Jos
.
Jos 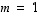 ,
typistyy summa muotoon
,
typistyy summa muotoon 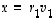 .
.
Edelleen vektorijoukon 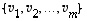 (jossa on vähintään kaksi vektoria) sanotaan olevan
lineaarisesti
riippuva (tai
sidottu), jos jokin niistä voidaan esittää muiden lineaarikombinaationa. Muussa tapauksessa kyseinen vektorijoukko on
lineaarisesti
riippumaton (eli
vapaa). Vektorijoukko on siis lineaarisesti riippumaton, jos mitään sen vektoreista ei voida esittää muiden vektoreiden lineaarikombinaationa. Vektorijoukon sijasta voidaan puhua myös sen vektoreiden lineaarisesta riippuvuudesta tai riippumattomuudesta.
(jossa on vähintään kaksi vektoria) sanotaan olevan
lineaarisesti
riippuva (tai
sidottu), jos jokin niistä voidaan esittää muiden lineaarikombinaationa. Muussa tapauksessa kyseinen vektorijoukko on
lineaarisesti
riippumaton (eli
vapaa). Vektorijoukko on siis lineaarisesti riippumaton, jos mitään sen vektoreista ei voida esittää muiden vektoreiden lineaarikombinaationa. Vektorijoukon sijasta voidaan puhua myös sen vektoreiden lineaarisesta riippuvuudesta tai riippumattomuudesta.
Opiskelutehtävä 7
Selvitä, ovatko vektorit 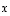 ja
ja 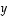 lineaarisesti riippuvat vai riippumattomat, kun
lineaarisesti riippuvat vai riippumattomat, kun
(a) 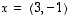 ja
ja 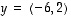 ,
,
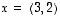 ja
ja 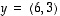 ,
,
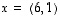 ja
ja 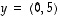 .
.
Miten kahden vektorin riippuvuus tai riippumattomuus on helposti nähtävissä?
Vinkki tehtävään 7
Jos jokin vektori voidaan lausua muiden lineaarikombinaationa, tarkasteltava vektorijoukko on määritelmän mukaan lineaarisesti riippuva. Mutta se, onko jokin vektori - ja mikä niistä - muiden lineaarikombinaatio, voi olla vaikea keksiä. Yksinkertaisesti voi olla ylivoimaista käydä kaikkia mahdollisuuksia läpi. Tarvitaan varmempia menetelmiä. Erään ratkaisun antaa seuraava tulos.
Lause 4.2.
Vektorijoukko 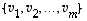 on lineaarisesti riippumaton, jos ja vain jos ehto
on lineaarisesti riippumaton, jos ja vain jos ehto
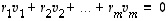
toteutuu ainoastaan kun 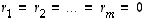 .
.
Todistus.
Tottakai 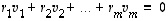 ,
mikäli
,
mikäli 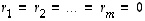 .
Mutta näin yksinkertaisesti ei toki väitetäkään! Yhtäpitävästi muotoiltuna väitetään nimittäin, että vektorijoukko
.
Mutta näin yksinkertaisesti ei toki väitetäkään! Yhtäpitävästi muotoiltuna väitetään nimittäin, että vektorijoukko 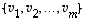 on lineaarisesti riippuva täsmälleen silloin, kun ehto
on lineaarisesti riippuva täsmälleen silloin, kun ehto 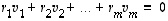 toteutuu myös, kun jokin kerroin
toteutuu myös, kun jokin kerroin 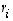 on nollasta eroava. Todistetaankin väite tässä muodossa.
on nollasta eroava. Todistetaankin väite tässä muodossa.
Jos 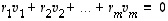 ja jokin
ja jokin 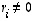 ,
esimerkiksi vaikka
,
esimerkiksi vaikka 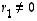 ,
silloin on
,
silloin on
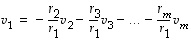
ja siten 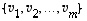 on lineaarisesti riippuva. Sama päättely toimii olipa mikä tahansa muu kerroin nollasta eroava. Tätä kerrointa vastaava vektori voidaan silloin lausua muiden lineaarikombinaationa.
on lineaarisesti riippuva. Sama päättely toimii olipa mikä tahansa muu kerroin nollasta eroava. Tätä kerrointa vastaava vektori voidaan silloin lausua muiden lineaarikombinaationa.
Edellä oleva päättely toimii kääntäenkin: Jos esimerkiksi vektori 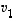 voidaan esittää muiden lineaarikombinaationa eli muodossa
voidaan esittää muiden lineaarikombinaationa eli muodossa 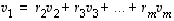 ,
on
,
on
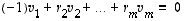 ,
,
missä ainakin vektorin 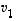 kerroin on nollasta eroava. Sama päättely toimii muunkin kuin ensimmäisen vektorin suhteen.
kerroin on nollasta eroava. Sama päättely toimii muunkin kuin ensimmäisen vektorin suhteen.

Yhden vektorin muodostamalle joukolle 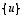 voidaan yllä olevan lauseen mukaisesti asettaa, että se on lineaarisesti riippumaton täsmälleen silloin, kun
voidaan yllä olevan lauseen mukaisesti asettaa, että se on lineaarisesti riippumaton täsmälleen silloin, kun 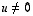 .
Pätee nimittäin, että
.
Pätee nimittäin, että
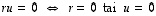 .
.
Kaksio 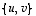 ,
missä
,
missä 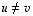 ,
on taas lineaarisesti riippumaton täsmälleen silloin, kun kumpikaan ei ole toisen monikerta. Jos kumpikaan niistä ei ole nollavektori, riippumattomuuden toteamiseen riittää, että toinen näistä vektoreista ei ole toisen monikerta. Ehto
,
on taas lineaarisesti riippumaton täsmälleen silloin, kun kumpikaan ei ole toisen monikerta. Jos kumpikaan niistä ei ole nollavektori, riippumattomuuden toteamiseen riittää, että toinen näistä vektoreista ei ole toisen monikerta. Ehto 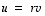 (kun
(kun 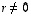 ) on nimittäin yhtäpitävä ehdon
) on nimittäin yhtäpitävä ehdon 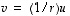 kanssa.
kanssa.
On myös helppo varmistua siitä, että mikään lineaarisesti riippumaton vektorijoukko ei voi ylipäätään sisältää nollavektoria.
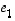 ja
ja 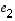 on todettu olevan sellainen erityinen ominaisuus, että mikä tahansa tason vektori voidaan yksikäsitteisesti esittää näiden lineaarikombinaationa. Tasossa on kuitenkin muitakin vektoreita, joilla on samanlainen 'kantaominaisuus´. Esimerkiksi, jos
on todettu olevan sellainen erityinen ominaisuus, että mikä tahansa tason vektori voidaan yksikäsitteisesti esittää näiden lineaarikombinaationa. Tasossa on kuitenkin muitakin vektoreita, joilla on samanlainen 'kantaominaisuus´. Esimerkiksi, jos 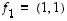 ja
ja 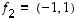 ,
jokaisella vektorilla
,
jokaisella vektorilla 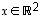 on mitä ilmeisimmin jokin esitys
on mitä ilmeisimmin jokin esitys 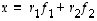 .
Itse asiassa tämä voidaan varmentaa laskemalla: jos
.
Itse asiassa tämä voidaan varmentaa laskemalla: jos 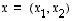 ,
valitsemalla
,
valitsemalla 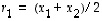 ja
ja 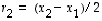 saadaan yhtälö
saadaan yhtälö 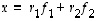 toteutumaan. Nämä kertoimet ovat kaiken lisäksi ainoat mahdolliset. Geometrisesti tämäkin on varsin selvää ja se voidaan toisaalta myös todentaa ratkaisemalla kertoimet yhtälöstä
toteutumaan. Nämä kertoimet ovat kaiken lisäksi ainoat mahdolliset. Geometrisesti tämäkin on varsin selvää ja se voidaan toisaalta myös todentaa ratkaisemalla kertoimet yhtälöstä 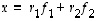 (missä vektorien
(missä vektorien 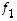 ja
ja 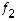 paikoille on ensin sijoitettu annetut lukuparit).
paikoille on ensin sijoitettu annetut lukuparit). 
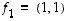 ja
ja 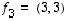 ,
tämä ei varmaankaan olisi käynyt! (Miksi?) Jos taas olisi valittu vektorit
,
tämä ei varmaankaan olisi käynyt! (Miksi?) Jos taas olisi valittu vektorit 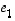 ,
,
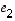 ja
ja 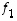 ,
kaikki tason vektorit voitaisiin kyllä ilmoittaa näiden lineaarikombinaationa valitsemalla yksinkertaisesti vektorin
,
kaikki tason vektorit voitaisiin kyllä ilmoittaa näiden lineaarikombinaationa valitsemalla yksinkertaisesti vektorin 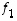 kertoimeksi aina nolla, mutta tämä esitystapa ei enää olisi suinkaan ainoa mahdollinen. Viimeksi mainittu vektori
kertoimeksi aina nolla, mutta tämä esitystapa ei enää olisi suinkaan ainoa mahdollinen. Viimeksi mainittu vektori 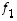 olisi siten tavallaan turha.
olisi siten tavallaan turha.  .
Siihen tarvitaan paria määrittelyä. Vektorin
.
Siihen tarvitaan paria määrittelyä. Vektorin 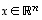 sanotaan olevan vektoreiden
sanotaan olevan vektoreiden 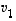 ,
,
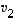 ,
...,
,
..., 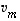 lineaarikombinaatio
lineaarikombinaatio 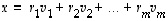
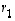 ,
,
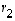 ,
...,
,
..., 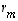 .
Jos
.
Jos 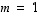 ,
typistyy summa muotoon
,
typistyy summa muotoon 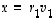 .
.
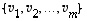 (jossa on vähintään kaksi vektoria) sanotaan olevan
lineaarisesti
(jossa on vähintään kaksi vektoria) sanotaan olevan
lineaarisesti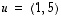 ja
ja 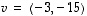 ,
on
,
on 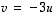 ja siten vektorijoukko
ja siten vektorijoukko 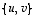 on lineaarisesti riippuva.
on lineaarisesti riippuva. 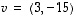 ,
niin selvästi
,
niin selvästi 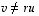 ja
ja 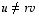 kaikilla reaaliluvuilla
kaikilla reaaliluvuilla 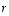 .
Niinpä
.
Niinpä 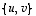 on nyt lineaarisesti riippumaton vektorijoukko.
on nyt lineaarisesti riippumaton vektorijoukko.
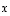 ja
ja 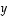 lineaarisesti riippuvat vai riippumattomat, kun
lineaarisesti riippuvat vai riippumattomat, kun 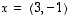 ja
ja 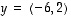 ,
,
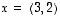 ja
ja 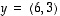 ,
,
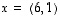 ja
ja 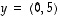 .
.
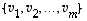 on lineaarisesti riippumaton, jos ja vain jos ehto
on lineaarisesti riippumaton, jos ja vain jos ehto 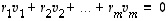
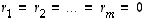 .
.
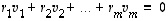 ,
mikäli
,
mikäli 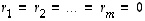 .
Mutta näin yksinkertaisesti ei toki väitetäkään! Yhtäpitävästi muotoiltuna väitetään nimittäin, että vektorijoukko
.
Mutta näin yksinkertaisesti ei toki väitetäkään! Yhtäpitävästi muotoiltuna väitetään nimittäin, että vektorijoukko 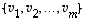 on lineaarisesti riippuva täsmälleen silloin, kun ehto
on lineaarisesti riippuva täsmälleen silloin, kun ehto 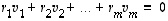 toteutuu myös, kun jokin kerroin
toteutuu myös, kun jokin kerroin 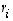 on nollasta eroava. Todistetaankin väite tässä muodossa.
on nollasta eroava. Todistetaankin väite tässä muodossa. 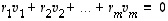 ja jokin
ja jokin 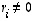 ,
esimerkiksi vaikka
,
esimerkiksi vaikka 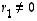 ,
silloin on
,
silloin on 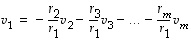
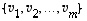 on lineaarisesti riippuva. Sama päättely toimii olipa mikä tahansa muu kerroin nollasta eroava. Tätä kerrointa vastaava vektori voidaan silloin lausua muiden lineaarikombinaationa.
on lineaarisesti riippuva. Sama päättely toimii olipa mikä tahansa muu kerroin nollasta eroava. Tätä kerrointa vastaava vektori voidaan silloin lausua muiden lineaarikombinaationa. 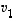 voidaan esittää muiden lineaarikombinaationa eli muodossa
voidaan esittää muiden lineaarikombinaationa eli muodossa 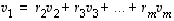 ,
on
,
on 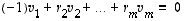 ,
,
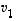 kerroin on nollasta eroava. Sama päättely toimii muunkin kuin ensimmäisen vektorin suhteen.
kerroin on nollasta eroava. Sama päättely toimii muunkin kuin ensimmäisen vektorin suhteen. 
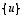 voidaan yllä olevan lauseen mukaisesti asettaa, että se on lineaarisesti riippumaton täsmälleen silloin, kun
voidaan yllä olevan lauseen mukaisesti asettaa, että se on lineaarisesti riippumaton täsmälleen silloin, kun 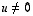 .
Pätee nimittäin, että
.
Pätee nimittäin, että 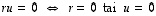 .
.
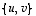 ,
missä
,
missä 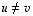 ,
on taas lineaarisesti riippumaton täsmälleen silloin, kun kumpikaan ei ole toisen monikerta. Jos kumpikaan niistä ei ole nollavektori, riippumattomuuden toteamiseen riittää, että toinen näistä vektoreista ei ole toisen monikerta. Ehto
,
on taas lineaarisesti riippumaton täsmälleen silloin, kun kumpikaan ei ole toisen monikerta. Jos kumpikaan niistä ei ole nollavektori, riippumattomuuden toteamiseen riittää, että toinen näistä vektoreista ei ole toisen monikerta. Ehto 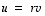 (kun
(kun 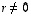 ) on nimittäin yhtäpitävä ehdon
) on nimittäin yhtäpitävä ehdon 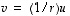 kanssa.
kanssa. 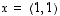 ja
ja 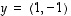 .
Selvitetään näiden tasovektorien lineaarinen riippuvuus ensin määrittelyn kautta eli katsomalla, milloin niiden lineaarikombinaatio on nollavektori. Päättelystä
.
Selvitetään näiden tasovektorien lineaarinen riippuvuus ensin määrittelyn kautta eli katsomalla, milloin niiden lineaarikombinaatio on nollavektori. Päättelystä 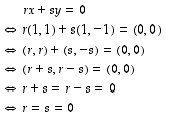
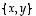 on lineaarisesti riippumaton. Sama voidaan nähdä toki suoraan siitä, että mikään (nollasta eroavan) vektorin
on lineaarisesti riippumaton. Sama voidaan nähdä toki suoraan siitä, että mikään (nollasta eroavan) vektorin 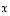 monikerta
monikerta 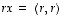 ei voi mitenkään antaa vektoria
ei voi mitenkään antaa vektoria 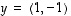 .
.

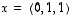 ,
,
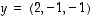 ja
ja 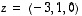 .
Selvitetään näiden avaruusvektoreiden lineaarinen riippuvuus katsomalla, milloin niiden lineaarikombinaatio on nollavektori. Nyt
.
Selvitetään näiden avaruusvektoreiden lineaarinen riippuvuus katsomalla, milloin niiden lineaarikombinaatio on nollavektori. Nyt 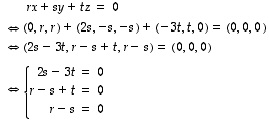
 .
.
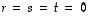 ,
mikä osoittaa, että vektorit
,
mikä osoittaa, että vektorit 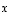 ,
,
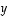 ja
ja 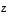 ovat lineaarisesti riippumattomat.
ovat lineaarisesti riippumattomat. 
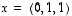 ,
,
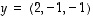 ja
ja 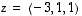 .
Selvitetään näiden avaruusvektoreiden lineaarinen riippuvuus katsomalla, milloin niiden lineaarikombinaatio on nollavektori. Nyt
.
Selvitetään näiden avaruusvektoreiden lineaarinen riippuvuus katsomalla, milloin niiden lineaarikombinaatio on nollavektori. Nyt 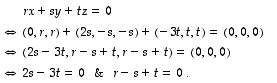
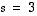 ja
ja 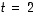 .
Toisesta yhtälöstä saadaan tämän jälkeen, että
.
Toisesta yhtälöstä saadaan tämän jälkeen, että 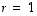 .
Tuloksena on, että ainakin yhtälö
.
Tuloksena on, että ainakin yhtälö 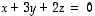 pätee. Tämä osoittaa, että vektorit
pätee. Tämä osoittaa, että vektorit 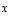 ,
,
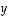 ja
ja 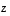 ovat lineaarisesti riippuvat. Samaan tulokseen olisi päästy heti suoraankin, jos vain olisi jotenkin arvattu, että
ovat lineaarisesti riippuvat. Samaan tulokseen olisi päästy heti suoraankin, jos vain olisi jotenkin arvattu, että 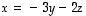 .
.

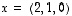 ja
ja 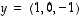 .
.
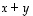 ja
ja 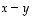 .
.
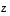 ,
joka on vektorien
,
joka on vektorien 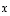 ja
ja 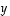 lineaarikombinaatio ja jonka kaksi ensimmäistä koordinaattia ovat erimerkkiset.
lineaarikombinaatio ja jonka kaksi ensimmäistä koordinaattia ovat erimerkkiset. 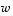 ,
joka ei ole vektorien
,
joka ei ole vektorien 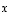 ja
ja 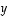 lineaarikombinaatio. Osoita sitten vektorit
lineaarikombinaatio. Osoita sitten vektorit 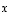 ,
,
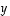 ja
ja 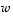 lineaarisesti riippumattomiksi.
lineaarisesti riippumattomiksi.