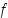 on jatkuva suljetulla välillä
on jatkuva suljetulla välillä 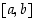 ja derivoituva avoimella välillä
ja derivoituva avoimella välillä 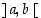 ,
niin avoimella välillä
,
niin avoimella välillä 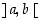 on piste
on piste 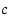 ,
jolle
,
jolle
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Kun Rollen lauseessa luovutaan ehdosta, jonka mukaan päätepistearvot ovat samat, saadaan yleisemmin seuraava tulos, jonka mukaan kuvaajalla on jossain välipisteessä sellainen tangentti, että sen kaltevuus on sama kuin kuvaajan päätepisteet yhdistävällä sekantilla.
Lause 4.1.3. (Differentiaalilaskennan väliarvolause (DVAL))
Jos funktio 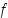 on jatkuva suljetulla välillä
on jatkuva suljetulla välillä 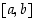 ja derivoituva avoimella välillä
ja derivoituva avoimella välillä 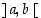 ,
niin avoimella välillä
,
niin avoimella välillä 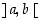 on piste
on piste 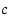 ,
jolle
,
jolle
Todistus. Suljetulla välillä 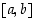 jatkuvalle ja vastaavalla avoimella välillä derivoituvalle funktiolle
jatkuvalle ja vastaavalla avoimella välillä derivoituvalle funktiolle
on 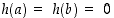 ,
joten Rollen lauseen mukaan on
,
joten Rollen lauseen mukaan on 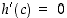 jollekin
jollekin 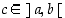 . Silloin
. Silloin
Differentiaalilaskennan väliarvolausetta kutsutaan myös Lagrangen väliarvolauseeksi. Sekä Rollen lause että väliarvolause osoittavat vain halutunlaisen välipisteen olemassaolon. Sen määräämiseen ne eivät anna yleistä keinoa. Siihen palataan ääriarvoteorian yhteydessä pykälässä Ääriarvot ja paikalliset ääriarvot.
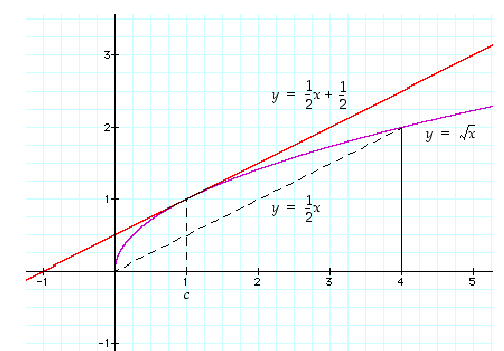
Tarkastellaan jatkuvaa funktiota 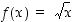 välillä
välillä 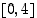 . Se on vastaavalla avoimella välillä derivoituva ja
. Se on vastaavalla avoimella välillä derivoituva ja
Differentiaalilaskennan väliarvolauseen oletukset ovat siten voimassa. Sen mukaisesti on olemassa piste 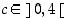 ,
jolle
,
jolle
Koska funktion 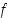 derivaatta tiedetään, voidaan piste
derivaatta tiedetään, voidaan piste 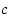 tässä tapauksessa määrätä: yhtälöstä
tässä tapauksessa määrätä: yhtälöstä 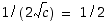 nähdään, että
nähdään, että 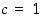 . Pisteessä
. Pisteessä 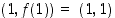 on siten kuvaajan tangentti, jonka yhtälö on
on siten kuvaajan tangentti, jonka yhtälö on 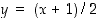 ,
saman suuntainen kuin pisteiden
,
saman suuntainen kuin pisteiden 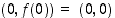 ja
ja 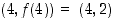 kautta kulkeva sekantti, joka on osa suoraa
kautta kulkeva sekantti, joka on osa suoraa 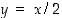 . Katso kuvaa 39.
. Katso kuvaa 39.
Opiskelutehtävä 22. (Differentiaalilaskennan väliarvolause)
differentiaalilaskennan väliarvolauseen oletukset välillä 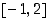 . Myönteisessä tapauksessa määrää jokin halutunlainen välipiste. Piirrä kuva!
. Myönteisessä tapauksessa määrää jokin halutunlainen välipiste. Piirrä kuva!
Oletetaan, että funktiosta 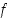 tiedetään, että
tiedetään, että 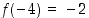 ,
,
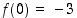 ja että välillä
ja että välillä 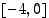 pätee
pätee 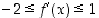 . Pyritään arvioimaan arvoa
. Pyritään arvioimaan arvoa 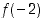 sekä alhaalta että ylhäältä.
sekä alhaalta että ylhäältä.
Tarkastellaan tilannetta ensin välin loppupisteestä päin. Differentiaalilaskennan väliarvolauseen mukaan jollekin 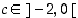 on
on
Koska 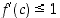 ,
on
,
on 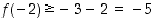 . Toisaalta
. Toisaalta 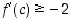 ,
joten
,
joten 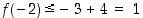 . Siten
. Siten 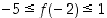 .
.
Arvioidaan arvoa 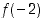 vastaavasti välin alkupisteestä lähtien. Väliarvolauseen mukaan jollekin
vastaavasti välin alkupisteestä lähtien. Väliarvolauseen mukaan jollekin 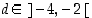 on nyt
on nyt
Ehdosta 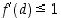 saadaan arvio
saadaan arvio 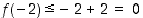 ja ehdosta
ja ehdosta 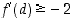 saadaan arvio
saadaan arvio 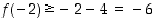 . Siten
. Siten 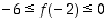 .
.
Saadut arviot yhdistämällä saadaan tulokseksi arvio 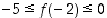 .
.
Väliarvolauseen avulla saadaan seuraava tulos, joka voi helpottaa toispuoleisten derivaattojen määräämistä välien reunapisteissä. Lauseen todistus jätetään harjoitustehtäväksi (tehtävä 127).
Oletetaan, että funktio 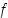 on jatkuva suljetulla välillä
on jatkuva suljetulla välillä 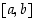 ,
derivoituva avoimella välillä
,
derivoituva avoimella välillä 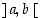 ja että derivaattakuvauksella
ja että derivaattakuvauksella 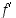 on pisteessä
on pisteessä 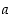 op. raja-arvona luku
op. raja-arvona luku 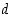 . Tällöin funktiolla
. Tällöin funktiolla 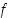 on pisteessä
on pisteessä 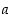 op. derivaatta
op. derivaatta 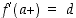 . Vastaava tulos pätee vasemmanpuoleiselle derivaatoille.
. Vastaava tulos pätee vasemmanpuoleiselle derivaatoille.
Seuraava lause on väliarvolauseen yleistys rationaalilausekkeille.
Lause 4.1.7. (Yleistetty differentiaalilaskennan väliarvolause)
Olkoot funktiot 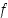 ja
ja 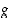 jatkuvia suljetulla välillä
jatkuvia suljetulla välillä 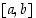 ja derivoituvia avoimella välillä
ja derivoituvia avoimella välillä 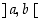 . Jos lisäksi
. Jos lisäksi 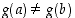 sekä derivaatat
sekä derivaatat 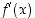 ja
ja 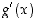 eivät ole missään pisteessä yhtaikaa nollia, niin avoimella välillä
eivät ole missään pisteessä yhtaikaa nollia, niin avoimella välillä 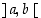 on piste
on piste 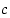 ,
jolle
,
jolle
Todistus. Väite osoitetaan samaan tapaan kuin tavallinen väliarvolause tarkastelemalla nyt vain funktiota
Yksityiskohtainen todistus sivuutetaan tässä.
Yleistettyä differentiaalilaskennan väliarvolausetta kutsutaan myös Cauchyn väliarvolauseeksi.