 on jatkuva suljetulla välillä
on jatkuva suljetulla välillä 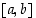 ,
derivoituva avoimella välillä
,
derivoituva avoimella välillä 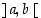 ja
ja 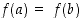 ,
niin avoimella välillä
,
niin avoimella välillä 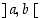 on piste
on piste 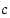 ,
jolle
,
jolle 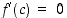 .
.
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Osoitetaan ensin, että jos derivoituva funktio saa välin päätepisteissä yhtä suuret arvot, on sillä jossain kohtaa vaakasuora tangentti eli sen derivaatta on jossain pisteessä nolla.
Jos funktio 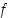 on jatkuva suljetulla välillä
on jatkuva suljetulla välillä 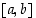 ,
derivoituva avoimella välillä
,
derivoituva avoimella välillä 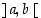 ja
ja 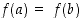 ,
niin avoimella välillä
,
niin avoimella välillä 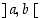 on piste
on piste 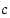 ,
jolle
,
jolle 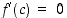 .
.
Todistus. Jos funktio 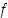 on vakio koko välillä
on vakio koko välillä 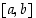 ,
on sen derivaatta nolla koko välillä
,
on sen derivaatta nolla koko välillä 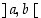 ja siten mikä tahansa sen piste kelpaa halutuksi pisteeksi
ja siten mikä tahansa sen piste kelpaa halutuksi pisteeksi 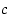 .
.
Oletetaan sitten, että funktio 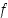 saa välillä
saa välillä 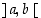 suurempia arvoja kuin päätepisteissä, ks. kuva 37. Weierstrassin lauseen mukaan on piste
suurempia arvoja kuin päätepisteissä, ks. kuva 37. Weierstrassin lauseen mukaan on piste 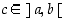 ,
jossa
,
jossa 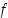 saa suurimman arvonsa. Oletuksen mukaan
saa suurimman arvonsa. Oletuksen mukaan 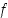 on derivoituva pisteessä
on derivoituva pisteessä 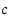 . Osoitetaan, että
. Osoitetaan, että 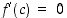 .
.
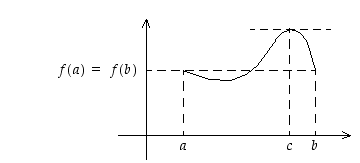
Kun 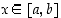 ,
niin
,
niin 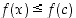 ja siten
ja siten 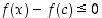 . Jos lisäksi
. Jos lisäksi 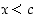 ,
on
,
on 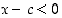 . Näin ollen derivaatalle
. Näin ollen derivaatalle 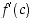 saadaan arvio
saadaan arvio
Jos taas 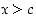 ,
on
,
on 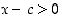 ,
ja siten derivaatalle
,
ja siten derivaatalle 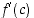 saadaan nyt arvio
saadaan nyt arvio
Näin ollen 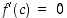 ja väitetty tilanne on saavutettu.
ja väitetty tilanne on saavutettu.
Tapaus, jossa  saa välillä
saa välillä  (vain) pienempiä arvoja kuin päätepisteissä, käsitellään vastaavasti.
(vain) pienempiä arvoja kuin päätepisteissä, käsitellään vastaavasti.
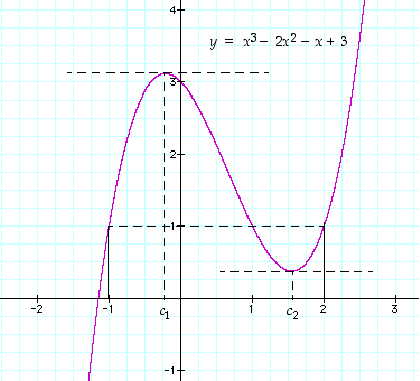
Tarkastellaan funktiota 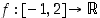 ,
,
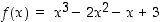 . Se on polynomina (kaikkialla) jatkuva ja derivoituva ja sille
. Se on polynomina (kaikkialla) jatkuva ja derivoituva ja sille 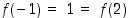 ,
joten Rollen lauseen oletukset ovat sille voimassa. Sen mukaan on olemassa piste
,
joten Rollen lauseen oletukset ovat sille voimassa. Sen mukaan on olemassa piste 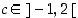 ,
jolle
,
jolle 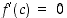 . Tällainen piste pystytään nyt myös määräämään. Koska
. Tällainen piste pystytään nyt myös määräämään. Koska 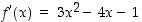 ,
niin yhtälöstä
,
niin yhtälöstä 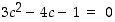 saadaan ratkaisuiksi
saadaan ratkaisuiksi
Molemmat ratkaisut ovat välillä 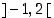 ,
joten itse asiassa nyt on olemassa kaksi eri pistettä, jossa derivaatta on nolla. Katso kuvaa 38.
,
joten itse asiassa nyt on olemassa kaksi eri pistettä, jossa derivaatta on nolla. Katso kuvaa 38.