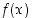 on derivoituva pisteessä
on derivoituva pisteessä 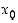 ,
jolloin määritelmän mukaan
,
jolloin määritelmän mukaan
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Tarkastellaan lähemmin funktion kuvaajan approksimointia sen tangenteilla. Oletetaan, että funktio 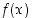 on derivoituva pisteessä
on derivoituva pisteessä 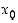 ,
jolloin määritelmän mukaan
,
jolloin määritelmän mukaan
Tämä voidaan kirjoittaa muotoon
Merkitsemällä sulkeiden sisällä olevaa lauseketta muuttujasta 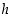 riippuvalla funktiolla
riippuvalla funktiolla 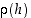 ,
ts.
,
ts.
jossa siis 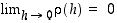 . Kun sovitaan lisäksi, että
. Kun sovitaan lisäksi, että 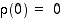 ,
on saatu osoitettua toinen puoli seuraavasta tuloksesta.
,
on saatu osoitettua toinen puoli seuraavasta tuloksesta.
Funktio 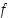 on derivoituva pisteessä
on derivoituva pisteessä 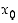 täsmälleen silloin, kun sillä on siinä pisteessä differentiaalikehitelmä
täsmälleen silloin, kun sillä on siinä pisteessä differentiaalikehitelmä
missä 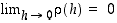 ja
ja 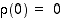 . Tällaisessa tapauksessa
. Tällaisessa tapauksessa 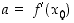 .
.
Todistus. Differentiaalikehitelmän olemassaolo pisteessä 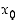 derivoituvalle funktiolle tuli edellä perusteltua. Oletetaan nyt, että kyseinen kehitelmä on olemassa, ja osoitetaan, että funktio
derivoituvalle funktiolle tuli edellä perusteltua. Oletetaan nyt, että kyseinen kehitelmä on olemassa, ja osoitetaan, että funktio 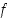 on derivoituva pisteessä
on derivoituva pisteessä 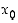 . Kehitelmän olemassaolosta seuraa, että erotusosamäärä on muotoa
. Kehitelmän olemassaolosta seuraa, että erotusosamäärä on muotoa
Tämän raja-arvoksi, kun 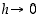 ,
nähdään tästä luku
,
nähdään tästä luku 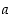 . Niinpä funktio
. Niinpä funktio 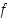 on derivoituva pisteessä
on derivoituva pisteessä 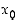 ja
ja 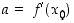 .
.
Määrätään funktiolle 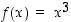 differentiaalikehitelmiä eri pisteissä. Tarkastellaan ensin pistettä
differentiaalikehitelmiä eri pisteissä. Tarkastellaan ensin pistettä 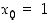 . Silloin
. Silloin
Tästä nähdään, että luku 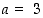 ja lauseke
ja lauseke 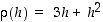 toteuttavat differentiaalikehitelmän vaatimukset. Siten
toteuttavat differentiaalikehitelmän vaatimukset. Siten 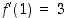 .
.
Yleisesti pisteessä 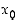 saadaan vastaavasti
saadaan vastaavasti
Tästä nähdään, että luku 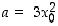 ja lauseke
ja lauseke 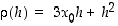 toteuttavat nyt differentiaalikehitelmän vaatimukset ja siten
toteuttavat nyt differentiaalikehitelmän vaatimukset ja siten 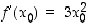 .
.
Differentiaalikehitelmän avulla voidaan periaatteessa määrätä funktion derivaatta. Tämä ei ole kuitenkaan yleisesti käytännöllistä, vaan seuraavassa pykälässä ja myöhemminkin johdamme parempia menetelmiä derivaatan määräämiseen.
Opiskelutehtävä 19. (Differentiaalikehitelmä)
(a) Muodosta funktion 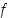 differentiaalikehitelmä pisteessä
differentiaalikehitelmä pisteessä 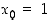 . Mitkä ovat tällöin luku
. Mitkä ovat tällöin luku 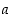 ja funktio
ja funktio 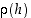 ?
?
(b) Muodosta funktion 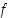 differentiaalikehitelmä yleisessä pisteessä
differentiaalikehitelmä yleisessä pisteessä 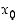 . Mitkä ovat tällöin luku
. Mitkä ovat tällöin luku 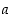 ja funktio
ja funktio 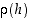 ?
?
(c) Mitkä ovat differentiaalikehitelmän perusteella funktion 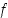 derivaatat pisteissä 1 ja
derivaatat pisteissä 1 ja 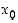 ?
?