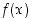 on jatkuva suljetulla välillä
on jatkuva suljetulla välillä 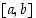 ja luku
ja luku 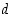 on arvojen
on arvojen 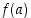 ja
ja 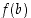 välissä, saa se avoimella välillä
välissä, saa se avoimella välillä 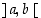 arvon
arvon 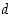 ,
ts. on olemassa piste
,
ts. on olemassa piste 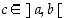 ,
jolle
,
jolle 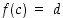 .
.
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Seuraavassa Bolzanon lause yleistetään koskemaan muitakin "väliarvoja" kuin nollaa.
Lause 2.4.3. (Jatkuvien funktioiden väliarvolause (JVAL))
Jos funktio 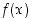 on jatkuva suljetulla välillä
on jatkuva suljetulla välillä 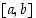 ja luku
ja luku 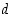 on arvojen
on arvojen 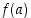 ja
ja 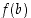 välissä, saa se avoimella välillä
välissä, saa se avoimella välillä 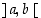 arvon
arvon 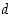 ,
ts. on olemassa piste
,
ts. on olemassa piste 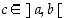 ,
jolle
,
jolle 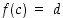 .
.
Todistus. Tarkastellaan funktiota 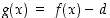 (ks. kuva 31).
(ks. kuva 31).
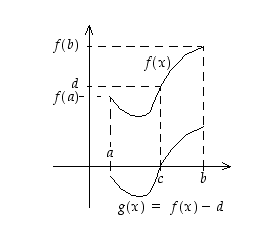
Se on jatkuva välillä 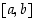 ja sille arvot
ja sille arvot 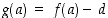 ja
ja 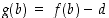 ovat oletuksen johdosta erimerkkiset. Siten se toteuttaa Bolzanon lauseen ehdot. On siis olemassa piste
ovat oletuksen johdosta erimerkkiset. Siten se toteuttaa Bolzanon lauseen ehdot. On siis olemassa piste 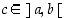 ,
jolle
,
jolle 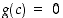 . Mutta silloinhan
. Mutta silloinhan 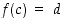 .
.
Seuraava tulos ei ole todistettavissa tämän esityksen tiedoin, joten se annetaan käyttöön ilman todistusta!
Lause 2.4.4. (Weierstrassin lause)
Suljetulla välillä 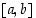 jatkuva funktio
jatkuva funktio 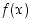 saa tällä välillä suurimman ja pienimmän arvonsa,
ts. on olemassa pisteet
saa tällä välillä suurimman ja pienimmän arvonsa,
ts. on olemassa pisteet 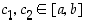 ,
joille
,
joille
Jatkuvien funktioiden väliarvolause huomioiden Weierstrassin lauseen sisältö voidaan lausua myös seuraavasti.
Jatkuva funktio kuvaa suljetun välin suljetuksi väliksi.
Todistus. Weierstrassin lauseen merkinnöin on jatkuvien funktioiden väliarvolauseen perusteella 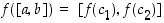 ,
mikä ilmaiseekin väitteen oikeaksi.
,
mikä ilmaiseekin väitteen oikeaksi.
Funktio 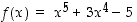 on polynomina kaikkialla jatkuva funktio. Edellisen tuloksen mukaan esimerkiksi välin
on polynomina kaikkialla jatkuva funktio. Edellisen tuloksen mukaan esimerkiksi välin 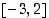 kuvajoukko
kuvajoukko 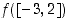 on suljettu väli. Millainen se on?
on suljettu väli. Millainen se on?
Esimerkissä 2.4.2 on laskettu, että 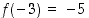 ,
,
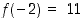 ,
,
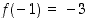 ,
,
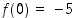 ,
,
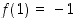 ja
ja 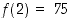 . Tämän mukaan kysytty kuvajoukko sisältää ainakin välin
. Tämän mukaan kysytty kuvajoukko sisältää ainakin välin 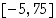 . Avoimeksi kysymykseksi jää kuitenkin tässä vaiheessa, voidaanko funktiolle löytää tällä välillä isompia tai pienempiä arvoja.
. Avoimeksi kysymykseksi jää kuitenkin tässä vaiheessa, voidaanko funktiolle löytää tällä välillä isompia tai pienempiä arvoja.
Opiskelutehtävä 16. (Funktion arvon saavuttaminen)
Osoita, että funktio 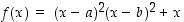 saa arvon
saa arvon 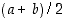 jossain pisteessä
jossain pisteessä 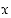 .
.
Weierstrassin lause on pelkkä olemassaolotulos; se ei anna mitään keinoa minimi- ja maksimikohtien etsimiseen. Haarukoinnilla, kuten esimerkiksi välien puolittamisella, voidaan näitä kohtia approksimoida likimääräisesti. Luvussa Funktion käyttäytyminen todetaan jatkuvia funktioita säännöllisimmille funktioille toimivia menetelmiä ääriarvokohtien löytämiseksi. Geometrisesti tämä johtaa kuvaajan tangenttien selvittämiseen ja sitä kautta derivaatan käsitteeseen.