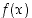 on jatkuva suljetulla välillä
on jatkuva suljetulla välillä 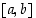 ja sen arvot päätepisteissä ovat erimerkkiset, ts.
ja sen arvot päätepisteissä ovat erimerkkiset, ts. 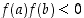 ,
on sillä avoimella välillä
,
on sillä avoimella välillä 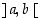 nollakohta, ts. piste
nollakohta, ts. piste 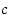 ,
jolle
,
jolle 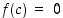 .
.
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Jatkuvan funktion käyttäytymisestä suljetulla välillä voidaan tehdä useita päätelmiä. Sen kuvaajaa ajatellen on ilmeistä, että välin päätepisteissä saatujen arvojen lisäksi se saa kaikki niiden välillä olevat arvot. Edelleen ilmeistä on, että jos sillä on mitkä tahansa "isot" ja "pienet" arvot, se saa myös kaikki niiden väliset arvot. Entä, onko "isoista isointa" tai "pienistä pienintä" arvoa olemassa? Toisin sanoen, saako jatkuva funktio aina maksimiarvonsa ja minimiarvonsa? Seuraavassa tarkastelemme näitä kysymyksiä.
Ensimmäinen huomio on, että jos jatkuva funktio saa sekä positiivisen arvon että negatiivisen arvon, saa se myös arvon nolla.
Jos funktio 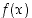 on jatkuva suljetulla välillä
on jatkuva suljetulla välillä 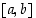 ja sen arvot päätepisteissä ovat erimerkkiset, ts.
ja sen arvot päätepisteissä ovat erimerkkiset, ts. 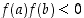 ,
on sillä avoimella välillä
,
on sillä avoimella välillä 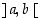 nollakohta, ts. piste
nollakohta, ts. piste 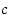 ,
jolle
,
jolle 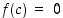 .
.
Todistus. Oletetaan, että 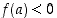 ja
ja 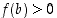 ,
vastaavasti voidaan todistaa päinvastainen tapaus. Tarkastellaan joukkoa
,
vastaavasti voidaan todistaa päinvastainen tapaus. Tarkastellaan joukkoa
Se ei ole tyhjä joukko, sillä ainakin luku 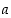 sisältyy siihen, ja toisaalta se on ylhäältä rajoitettu luvulla
sisältyy siihen, ja toisaalta se on ylhäältä rajoitettu luvulla 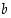 . Täydellisyysaksiooman mukaan sillä on siten pienin yläraja; olkoon
. Täydellisyysaksiooman mukaan sillä on siten pienin yläraja; olkoon 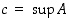 (ks. kuva 30).
(ks. kuva 30).
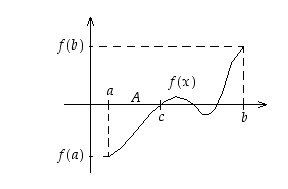
Kun 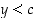 ,
on
,
on 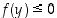 ,
joten jatkuvuuden perusteella on
,
joten jatkuvuuden perusteella on
Jos olisi 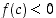 ,
olisi merkin säilyvyyden perusteella
,
olisi merkin säilyvyyden perusteella 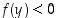 jollain välillä
jollain välillä 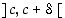 . Silloin olisi
. Silloin olisi 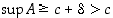 ,
mikä on ristiriita. On siis oltava
,
mikä on ristiriita. On siis oltava 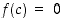 ,
mikä osoittaakin lauseen väitteen oikeaksi.
,
mikä osoittaakin lauseen väitteen oikeaksi.
On selvää, että Bolzanon lauseessa funktion jatkuvuus on olennaista: epäjatkuvan funktion kuvaaja voi "hypätä" vaaka-akselin yli. Bolzanon lause ilmaiseekin, että "jatkuva funktio ei voi vaihtaa merkkiään käymättä nollan kautta". Lausetta voi soveltaa jatkuvalle funktiolle jokaisella suljetulla välillä, jolla se on määritelty kokonaan.
Tutkitaan funktion 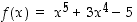 nollakohtia. Se on polynomina kaikkialla jatkuva funktio. Kokeillaan laskea funktion arvoja esimerkiksi kokonaislukupisteissä:
nollakohtia. Se on polynomina kaikkialla jatkuva funktio. Kokeillaan laskea funktion arvoja esimerkiksi kokonaislukupisteissä:
Funktio vaihtaa siten merkkiään väleillä 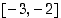 ,
,
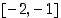 ja
ja 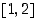 . Vastaavilla avoimilla väleillä on siten nollakohta. Ainakin yksi kullakin. Lause ei kuitenkaan suoraan ilmaise, onko nollakohtia näillä väleillä yksi vai useampia. Viidennen asteen polynomillahan voi olla enimmillään viisi juurta.
. Vastaavilla avoimilla väleillä on siten nollakohta. Ainakin yksi kullakin. Lause ei kuitenkaan suoraan ilmaise, onko nollakohtia näillä väleillä yksi vai useampia. Viidennen asteen polynomillahan voi olla enimmillään viisi juurta.
Nollakohtien sijaintia voidaan kuitenkin tarkentaa haarukoinnilla eli jakamalla välejä pienempiin osiin. Voi vaikkapa puolittaa välin ja katsoa kummalla puolella funktion merkki muuttuu. Koska funktiolle 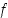 on esimerkiksi
on esimerkiksi 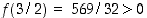 ,
on nollakohta välin
,
on nollakohta välin 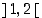 sijasta tarkemmin välillä
sijasta tarkemmin välillä 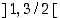 .
.
Tarkasteltavan polynomifunktion 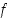 nollakohdille ei ole määrättävissä tarkkoja lausekkeita, mutta likiarvoiset nollakohdat ovat
nollakohdille ei ole määrättävissä tarkkoja lausekkeita, mutta likiarvoiset nollakohdat ovat 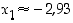 ,
,
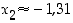 ja
ja 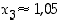 .
.