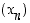 monikertajono
monikertajono 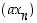 ,
missä
,
missä 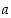 on vakio, tarkoittaa jonoa
on vakio, tarkoittaa jonoa
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Jonon 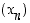 monikertajono
monikertajono 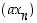 ,
missä
,
missä 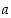 on vakio, tarkoittaa jonoa
on vakio, tarkoittaa jonoa
Kahden jonon 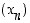 ja
ja 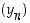 summajono on jono
summajono on jono
Vastaavasti näiden jonojen tulojono on jono
edellyttäen, että kaikki osamäärät ovat määriteltyjä ts. 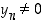 . Näiden jonojen suppenemisesta ilmaisee seuraava lause.
. Näiden jonojen suppenemisesta ilmaisee seuraava lause.
Lause 2.1.7. (Raja-arvojen rationaaliset laskusäännöt)
Jos jonot 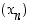 ja
ja 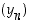 suppenevat, niin myös jonot
suppenevat, niin myös jonot 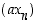 (kaikilla luvuilla
(kaikilla luvuilla 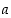 ),
), 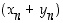 ,
,
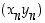 ja
ja 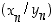 (mikäli kyseiset osamäärät on määritelty ja
(mikäli kyseiset osamäärät on määritelty ja 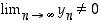 ) suppenevat ja erityisesti
) suppenevat ja erityisesti
Todistus. Olkoot 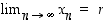 ja
ja 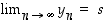 . Jos
. Jos 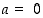 ,
on
,
on 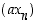 nollista muodostuva vakiojono ja suppenee siten kohti nollaa. Olkoon sitten
nollista muodostuva vakiojono ja suppenee siten kohti nollaa. Olkoon sitten 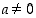 . Jonon
. Jonon 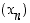 suppenevuuden perusteella on jokaiselle positiiviselle luvulle
suppenevuuden perusteella on jokaiselle positiiviselle luvulle 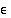 olemassa sellainen indeksi
olemassa sellainen indeksi 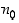 ,
että
,
että 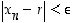 aina, kun
aina, kun 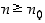 . Silloin
. Silloin 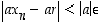 ,
joten erotus
,
joten erotus 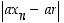 saadaan mielivaltaisen pieneksi. Tästä päätellään, että
saadaan mielivaltaisen pieneksi. Tästä päätellään, että 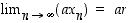 .
.
Todistetaan sitten summajonon raja-arvoa koskeva väite. Jonojen 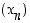 ja
ja 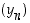 suppenevuuksien perusteella on jokaiselle positiiviselle luvulle
suppenevuuksien perusteella on jokaiselle positiiviselle luvulle 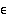 olemassa sellainen indeksi
olemassa sellainen indeksi 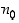 ,
että
,
että 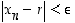 ja
ja 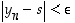 aina, kun
aina, kun 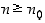 . Siten
. Siten
Seuraavaksi todistetaan tulojonon raja-arvoa koskeva väite. Edellä olevin merkinnöin on
Vielä on todistettava osamäärän raja-arvoa koskeva väite. Tulon raja-arvoa hyväksi käyttäen riittää osoittaa, että jono 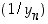 suppenee ja että sen raja-arvo on
suppenee ja että sen raja-arvo on 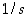 . Edellä olevin merkinnöin on
. Edellä olevin merkinnöin on
Koska 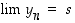 ja
ja 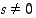 ,
on olemassa sellainen indeksi
,
on olemassa sellainen indeksi 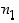 ,
että
,
että 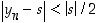 aina, kun
aina, kun 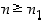 . Silloin
. Silloin 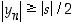 ja edelleen
ja edelleen
Tarkastellaan geometrisen jonon 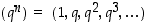 raja-arvoa. Tällaisessa jonossahan peräkkäisten termien suhde on vakio
raja-arvoa. Tällaisessa jonossahan peräkkäisten termien suhde on vakio 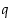 . Jos
. Jos 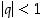 ,
on
,
on
kaikille luonnollisille luvuille 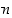 ,
joten jono
,
joten jono 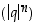 on alhaalta rajoitettu ja vähenevä. On siis olemassa raja-arvo
on alhaalta rajoitettu ja vähenevä. On siis olemassa raja-arvo
(tämä pätee myös, jos 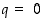 ). Silloin myös
). Silloin myös
Jos 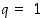 ,
niin jonon termit ovat kaikki ykkösiä ja siten se on myös raja-arvo.
,
niin jonon termit ovat kaikki ykkösiä ja siten se on myös raja-arvo.
Kun sitten 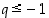 ,
jonon termien merkit vuorottelevat ja ovat itseisarvoltaan vähintään ykkösiä, joten jono ei voi supeta. Raja-arvoa ei siten ole olemassa.
,
jonon termien merkit vuorottelevat ja ovat itseisarvoltaan vähintään ykkösiä, joten jono ei voi supeta. Raja-arvoa ei siten ole olemassa.
Tulokseksi saatiin siten, että
Kuten pykälän alussa todettiin, jono on itse asiassa kuvaus 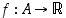 ,
missä
,
missä 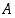 on jokin rajoittamaton peräkkäisten luonnollisten lukujen osajoukko. Kun seuraavassa pykälässä johdamme päättelysääntöjä yleensäkin funktioiden suppenemiselle, saamme siten samalla myös sääntöjä jonojen suppenemiselle.
on jokin rajoittamaton peräkkäisten luonnollisten lukujen osajoukko. Kun seuraavassa pykälässä johdamme päättelysääntöjä yleensäkin funktioiden suppenemiselle, saamme siten samalla myös sääntöjä jonojen suppenemiselle.