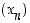 suppenee (eli konvergoi) kohti raja-arvoa
suppenee (eli konvergoi) kohti raja-arvoa 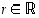 ,
jos jokaiselle positiiviselle (pienelle) luvulle
,
jos jokaiselle positiiviselle (pienelle) luvulle 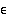 on olemassa sellainen indeksi
on olemassa sellainen indeksi 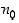 ,
että
,
että
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Edelleen määritellään, että lukujono 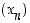 suppenee (eli konvergoi) kohti raja-arvoa
suppenee (eli konvergoi) kohti raja-arvoa 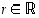 ,
jos jokaiselle positiiviselle (pienelle) luvulle
,
jos jokaiselle positiiviselle (pienelle) luvulle 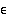 on olemassa sellainen indeksi
on olemassa sellainen indeksi 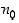 ,
että
,
että
(lim on lyhenne latinan sanasta limes) tai
Suppenemista varten ero 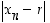 olisi siis saatava lopullisesti mielivaltaisen pieneksi eli edeltä annettua arvoa
olisi siis saatava lopullisesti mielivaltaisen pieneksi eli edeltä annettua arvoa 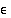 pienemmäksi. Vakiojonolle
pienemmäksi. Vakiojonolle 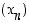 ,
missä
,
missä 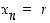 aina, kyseinen erotus on aina nolla, joten tällainen vakiojono suppenee kohti lukua
aina, kyseinen erotus on aina nolla, joten tällainen vakiojono suppenee kohti lukua 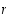 .
.
Määritelmästä näkyy, että lukujono suppenee lukua 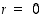 kohti täsmälleen silloin, kun sen itseisarvojono suppenee nollaan, ts.
kohti täsmälleen silloin, kun sen itseisarvojono suppenee nollaan, ts.
Nollaa kohti suppenevia jonoja sanotaan myös nollajonoiksi. Yleisesti jono 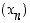 suppenee kohti raja-arvoa
suppenee kohti raja-arvoa 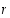 täsmälleen silloin, kun jono
täsmälleen silloin, kun jono 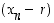 on nollajono.
on nollajono.
Jono 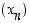 hajaantuu, jos se ei suppene mitään lukua kohti. Erityisesti se hajaantuu äärettömyyteen,
jos mille tahansa
hajaantuu, jos se ei suppene mitään lukua kohti. Erityisesti se hajaantuu äärettömyyteen,
jos mille tahansa 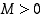 on olemassa sellainen indeksi
on olemassa sellainen indeksi 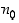 ,
että
,
että 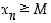 aina, kun
aina, kun 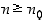 . Tämä merkitään
. Tämä merkitään
Vastaavasti määritellään hajaantuminen kohti miinus-ääretöntä 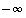 ,
ts. jono
,
ts. jono 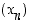 hajaantuu miinus-äärettömyyteen,
jos mille tahansa
hajaantuu miinus-äärettömyyteen,
jos mille tahansa 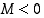 on olemassa sellainen indeksi
on olemassa sellainen indeksi 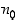 ,
että
,
että 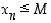 aina, kun
aina, kun 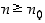 . Tämä merkitään
. Tämä merkitään
Huomaa, että jonon alkupään termit (äärelliseen määrään asti) eivät vaikuta jonon suppenemiseen tai hajaantumiseen.
(a) Jono 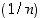 on aidosti vähenevä jono ja se suppenee kohti lukua 0, sillä
on aidosti vähenevä jono ja se suppenee kohti lukua 0, sillä 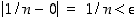 ,
kunhan
,
kunhan 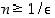 .
.
(b) Jono 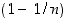 on aidosti kasvava jono ja suppenee kohti lukua 1, sillä
on aidosti kasvava jono ja suppenee kohti lukua 1, sillä
(c) Jono 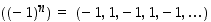 ei suppene, vaan hajaantuu.
ei suppene, vaan hajaantuu.
(d) Jono 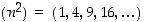 on aidosti kasvava ja hajaantuu kohti ääretöntä.
on aidosti kasvava ja hajaantuu kohti ääretöntä.
Selvitetään suppeneeko jono 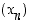 ,
kun
,
kun 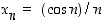 . Koska
. Koska 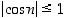 aina, on
aina, on
Tästä näkyy, että jono 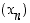 suppenee kohti nollaa.
suppenee kohti nollaa.
Reaalilukujen täydellisyysaksioomasta seuraa seuraava tulos.
Ylhäältä rajoitettu kasvava jono suppenee. Vastaavasti alhaalta rajoitettu vähenevä jono suppenee.
Todistus. Osoitetaan ylhäältä rajoitetun kasvavan jonon suppenevuus. Koska jonon alkioista muodostuva joukko 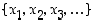 on ylhäältä rajoitettu, on sillä supremum, olkoon se
on ylhäältä rajoitettu, on sillä supremum, olkoon se 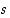 . Olkoon luku
. Olkoon luku 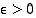 annettu. Silloin jollekin
annettu. Silloin jollekin 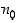 on
on 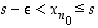 ,
sillä muutoin
,
sillä muutoin 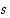 ei olisi supremum. Koska jono on kasvava, on siten
ei olisi supremum. Koska jono on kasvava, on siten 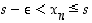 aina, kun
aina, kun 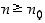 . Tällöin myös
. Tällöin myös 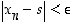 aina, kun
aina, kun 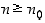 . Tämä osoittaa, paitsi suppenevuuden, myös sen, että raja-arvo on luku
. Tämä osoittaa, paitsi suppenevuuden, myös sen, että raja-arvo on luku 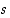 .
.
Selvitetään suppeneeko jono 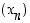 ,
kun
,
kun 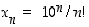 . Merkintä
. Merkintä 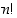 tarkoittaa
tarkoittaa 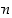 −kertomaa
−kertomaa 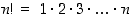 (jolle sovitaan lisäksi, että
(jolle sovitaan lisäksi, että 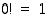 ). Jonon
). Jonon 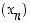 ensimmäiset termit ovat likimääräisesti
ensimmäiset termit ovat likimääräisesti 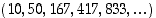 ,
joten näyttäisi, että jono on kasvava. Tarkastellaan tarkemmin perättäisten termien erotusta
,
joten näyttäisi, että jono on kasvava. Tarkastellaan tarkemmin perättäisten termien erotusta
Huomataan, että kun 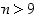 ,
suluissa oleva erotus on negatiivinen ja siten myös koko erotus
,
suluissa oleva erotus on negatiivinen ja siten myös koko erotus 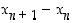 . Näin ollen jono
. Näin ollen jono 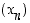 on vähenevä indeksistä
on vähenevä indeksistä 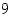 alkaen. Jonon
alkaen. Jonon 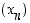 jäsenet ovat aina positiivisia, joten jono on alhaalta rajoitettu nollalla. Edellisen lauseen perusteella jono
jäsenet ovat aina positiivisia, joten jono on alhaalta rajoitettu nollalla. Edellisen lauseen perusteella jono 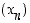 siis suppenee. Arvion
siis suppenee. Arvion
perusteella on ilmeistä, että tämän jonon raja-arvo on nolla. Tarkemmin tämä voidaan perustella funktioiden raja-arvoja käsittelevää kuristuslausetta 2.2.4 vastaavalla tuloksella jonoille tai vaihtoehtoisesti yleisen eksponenttifunktion käyttäytymisen avulla (ks. Eksponenttifunktio).
Opiskelutehtävä 11. (Lukujonon havainnollistus ja monotonisuus)
(a) Havainnollista jonoa 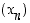 kuvalla (sijoita koordinaattitasoon luvun
kuvalla (sijoita koordinaattitasoon luvun 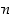 kohdalle arvo
kohdalle arvo 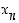 ).
).
(b) Onko jono 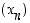 kasvava, vähenevä, monotoninen, aidosti kasvava, aidosti vähenevä, aidosti monotoninen, ylhäältä rajoitettu, alhaalta rajoitettu vai peräti rajoitettu?
kasvava, vähenevä, monotoninen, aidosti kasvava, aidosti vähenevä, aidosti monotoninen, ylhäältä rajoitettu, alhaalta rajoitettu vai peräti rajoitettu?
(c) Mitä raja-arvoa kohti jono 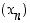 suppenee? Perustele väitteesi lukujonon suppenemisen määritelmää käyttäen.
suppenee? Perustele väitteesi lukujonon suppenemisen määritelmää käyttäen.
Opiskeluvideo: R1: Lukujonon raja-arvo 
