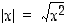Itseisarvofunktio

Esimerkissä 1.5.6 käytettiin itseisarvofunktiota 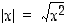(neliöjuurimerkinnällä tarkoitetaan aina epänegatiivista neliöjuurta), jolle siten

Esimerkki 1.5.7.

Määrätään 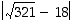. Koska 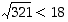− onha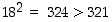n − on

.

Itseisarvofunktion eräs tärkeimmistä ominaisuuksista on ns. kolmioepäyhtälö

kaikille .

Kolmioepäyhtälö johdetaan seuraavasti. Koska 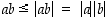, on

.

Ottamalla epäyhtälön molemmista puolista neliöjuuret saadaan haluttu epäyhtälö.

Erotuksen itseisarvo 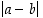ilmoittaa lukujen 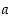ja 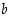etäisyyden. Erikoisesti itseisarvo 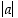on siis luvun 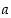etäisyys nollasta. Etäisyydelle pätee myös kolmioepäyhtälö muodossa

kaikille .

Tämä epäyhtälö saadaan itseisarvon kolmioepäyhtälöstä, kun etäisyys 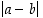kirjoitetaan muotoon .

Esimerkki 1.5.8.

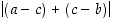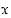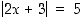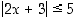Määrätään ne luvut , joille a) , b) ja c) .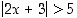

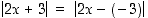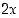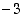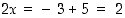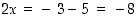a) Kun kirjoitetaan , huomataan, että luvun on oltava etäisyydellä 5 luvusta . Siten tai . Vastauksena on siis, että 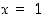tai .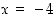

b) Edeltä nähdään, että epäyhtälö toteutuu, kun luku 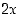on korkeintaan etäisyydellä 5 luvusta 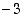. Siten 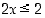ja 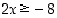. Vastauksena on siten, että .

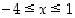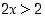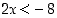c) Kuten edellä päätellään, että nyt on oltava tai . Vastauksena on siis, että 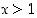tai 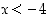.