 kuvaaja eli graafi on tason osajoukko
kuvaaja eli graafi on tason osajoukko
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Reaalifunktion 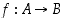 kuvaaja eli graafi on tason osajoukko
kuvaaja eli graafi on tason osajoukko
Funktion 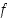 kuvaaja muodostuu siis niistä tason pisteistä
kuvaaja muodostuu siis niistä tason pisteistä 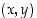 ,
joiden vaakakoordinaatti on
,
joiden vaakakoordinaatti on 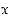 ja pystykoordinaatti on
ja pystykoordinaatti on 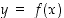 . Kuvaajaa
. Kuvaajaa 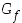 sanotaan myös käyräksi
sanotaan myös käyräksi 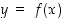 (ks. kuva 10).
(ks. kuva 10).
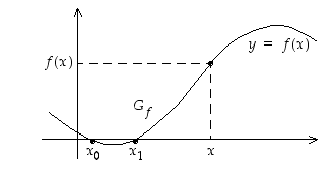
Funktion kuvaajan ja vaaka-akselin leikkauspisteet ovat funktion nollakohtia (kuvassa 10 pisteet 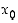 ja
ja 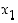 ovat eräitä nollakohtia). Huomaa, että kuhunkin funktion määrittelyjoukon pisteeseen liitetään vain yksi arvo, joten mikään tason pystysuora ei saa leikata kuvaajaa kahdessa (tai useammassa) eri kohdassa. Vaakasuorat voivat kyllä leikata kuvaajaa useissakin pisteissä, sillä funktio voi saada samoja arvoja eri pisteissä.
ovat eräitä nollakohtia). Huomaa, että kuhunkin funktion määrittelyjoukon pisteeseen liitetään vain yksi arvo, joten mikään tason pystysuora ei saa leikata kuvaajaa kahdessa (tai useammassa) eri kohdassa. Vaakasuorat voivat kyllä leikata kuvaajaa useissakin pisteissä, sillä funktio voi saada samoja arvoja eri pisteissä.
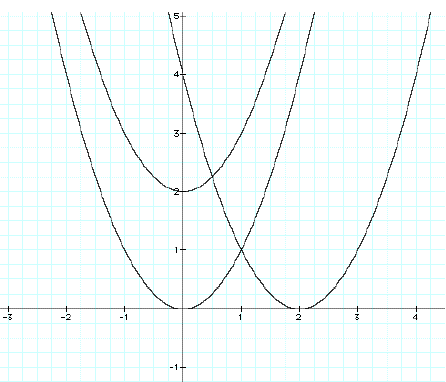
Kuvassa 11 on kuvattuna osat käyristä 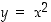 ,
,
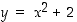 ja
ja 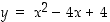 . Selvitä, mikä on mikin!
. Selvitä, mikä on mikin!
Oletetaan, että funktion 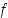 kuvaajalta on määrätty pisteet
kuvaajalta on määrätty pisteet 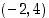 ,
,
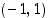 ,
,
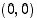 ,
,
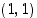 ja
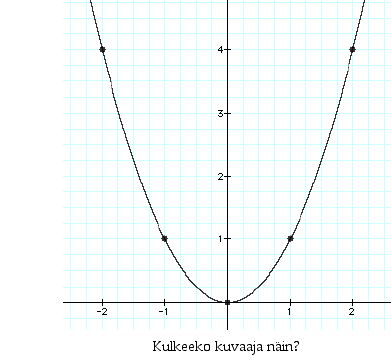
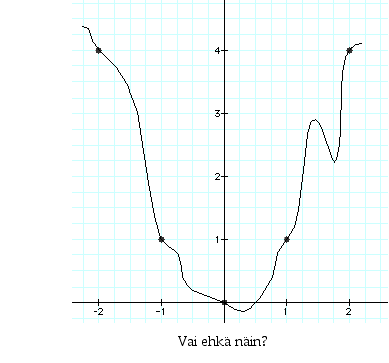
ja 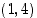 . Kuvaajalle on tämän perusteella tehty kuvassa kaksi hahmotelmaa, vasemmanpuoleinen "siisti" käyrä ja oikeanpuoleinen, jossa on paljon "mutkia". Mistä tiedämme, kumpi on oikeampi? Voimme tietenkin laskea lisäpisteitä kuvaajalta ja tarkentaa siten kuvaajan kulkua. Mutta tällä tavalla jää aina vierekkäisten laskentapisteiden väliin aukko, jossa kuvaajan kulku jää määräämättä. Miten tästä voidaan selvitä? Siihen tarvitaan juuri sitä funktion kulun selvittämisen analyysiä, jota jatkossa tulemme tekemään ja joka tulee antamaan luotettavuutta kuvaajan hahmottamiseen. Siihen tarvitsemme mm. funktion jatkuvuutta ja derivaattaa.
. Kuvaajalle on tämän perusteella tehty kuvassa kaksi hahmotelmaa, vasemmanpuoleinen "siisti" käyrä ja oikeanpuoleinen, jossa on paljon "mutkia". Mistä tiedämme, kumpi on oikeampi? Voimme tietenkin laskea lisäpisteitä kuvaajalta ja tarkentaa siten kuvaajan kulkua. Mutta tällä tavalla jää aina vierekkäisten laskentapisteiden väliin aukko, jossa kuvaajan kulku jää määräämättä. Miten tästä voidaan selvitä? Siihen tarvitaan juuri sitä funktion kulun selvittämisen analyysiä, jota jatkossa tulemme tekemään ja joka tulee antamaan luotettavuutta kuvaajan hahmottamiseen. Siihen tarvitsemme mm. funktion jatkuvuutta ja derivaattaa.
Funktio 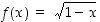 on määritelty, kun
on määritelty, kun 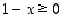 eli kun
eli kun 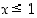 . Siten
. Siten 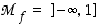 . Funktion
. Funktion 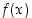 kuvaaja on hahmoteltu kuvassa 13.
kuvaaja on hahmoteltu kuvassa 13.
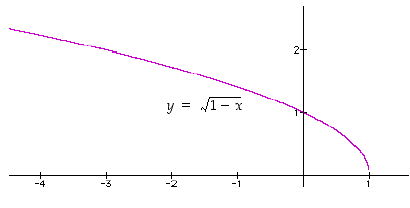
Olkoon lisäksi 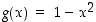 . Se on määritelty kaikkialla, ks. kuva 14.
. Se on määritelty kaikkialla, ks. kuva 14.
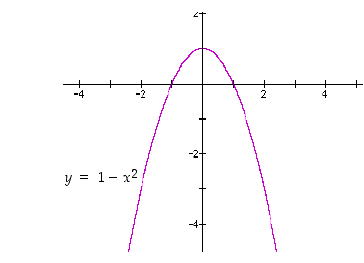
Tällöin yhdistetty kuvaus 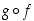 on määritelty välillä
on määritelty välillä 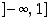 ja
ja
Yhdistetty kuvaus 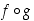 on taas määritelty silloin, kun
on taas määritelty silloin, kun 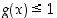 eli kun
eli kun 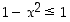 ,
siis kaikkialla. Lisäksi
,
siis kaikkialla. Lisäksi
Edeltä näkyy, että jos funktion 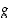 määrittelyalueeksi rajataan epänegatiiviset luvut eli väli
määrittelyalueeksi rajataan epänegatiiviset luvut eli väli 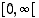 ,
tulee siitä silloin funktion
,
tulee siitä silloin funktion 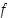 käänteisfunktio.
käänteisfunktio.
Jos kuvaukset on ilmoitettu lausekkeina, kuten edellisessä esimerkissä, on yhdistetty kuvaus 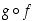 määritelty niissä pisteissä
määritelty niissä pisteissä 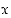 ,
jotka ensinnäkin kuuluvat kuvauksen
,
jotka ensinnäkin kuuluvat kuvauksen 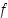 määrittelyjoukkoon ja toiseksi kuvautuvat kuvauksessa
määrittelyjoukkoon ja toiseksi kuvautuvat kuvauksessa 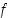 funktion
funktion 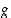 määrittelyjoukkoon.
määrittelyjoukkoon.
Opiskelutehtävä 5. (Funktion määritely- ja arvojoukko)
(a) Mikä on sen määrittelyjoukko 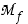 ?
?
(b) Osoita, että arvojoukko 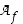 on rajoitettu.
on rajoitettu.
Laskentapohja: Yhdistetty funktio: Animaatio 1 
Laskentapohja: Yhdistetty funktio: Animaatio 2 