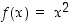 ,
missä
,
missä 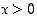 . Tällöin sen käänteisfunktio on
. Tällöin sen käänteisfunktio on 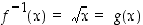 ,
jolle
,
jolle
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Tarkasteltava funktio on 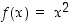 ,
missä
,
missä 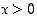 . Tällöin sen käänteisfunktio on
. Tällöin sen käänteisfunktio on 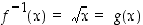 ,
jolle
,
jolle
Siten funktion 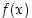 käänteisfunktion derivaatta kohdassa 2 on
käänteisfunktion derivaatta kohdassa 2 on
Sama tulos saadaan (implisiittisesti) käyttämällä käänteiskuvauksen derivointisääntöä
missä 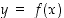 . Jotta sääntöä voidaan hyödyntää, tulee huomata, että kun
. Jotta sääntöä voidaan hyödyntää, tulee huomata, että kun 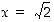 ,
niin
,
niin 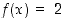 . Lisäksi tarvitaan tietoa, että
. Lisäksi tarvitaan tietoa, että 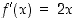 . Täten siis
. Täten siis
[Opiskelutehtävä 25.] [Vinkki tehtävään 25]