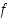 derivoituva avoimella välillä
derivoituva avoimella välillä 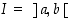 sekä sen derivaatta joko positiivinen koko välillä
sekä sen derivaatta joko positiivinen koko välillä  tai negatiivinen koko välillä
tai negatiivinen koko välillä 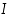 . Tällöin käänteiskuvaus
. Tällöin käänteiskuvaus 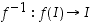 on derivoituva avoimella välillä
on derivoituva avoimella välillä 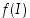 . Lisäksi derivaatalle pätee lauseke
. Lisäksi derivaatalle pätee lauseke
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Seuraavaksi tarkastelemme derivoituvuuden periytymistä käänteisfunktiolle.
Lause 4.4.3. (Käänteiskuvauksen derivoituvuus)
Olkoon funktio 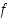 derivoituva avoimella välillä
derivoituva avoimella välillä 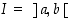 sekä sen derivaatta joko positiivinen koko välillä
sekä sen derivaatta joko positiivinen koko välillä 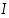 tai negatiivinen koko välillä
tai negatiivinen koko välillä 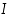 . Tällöin käänteiskuvaus
. Tällöin käänteiskuvaus 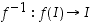 on derivoituva avoimella välillä
on derivoituva avoimella välillä 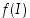 . Lisäksi derivaatalle pätee lauseke
. Lisäksi derivaatalle pätee lauseke
Todistus. Derivoituvana funktiona 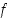 on jatkuva ja derivaatan positiivisuudesta (tai negatiivisuudesta) seuraa funktion
on jatkuva ja derivaatan positiivisuudesta (tai negatiivisuudesta) seuraa funktion 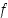 aito monotonisuus. Edellisen lauseen 4.4.2 mukaan kuvajoukko
aito monotonisuus. Edellisen lauseen 4.4.2 mukaan kuvajoukko 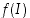 on väli sekä käänteiskuvaus
on väli sekä käänteiskuvaus 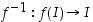 on aidosti monotoninen ja jatkuva.
on aidosti monotoninen ja jatkuva.
Derivoituvuus perustellaan erotusosamäärän kautta. Kun 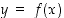 ja
ja 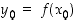 ,
saadaan
,
saadaan
Koska 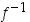 on jatkuva, seuraa ehdosta
on jatkuva, seuraa ehdosta 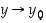 ehto
ehto 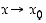 . Siten erotusosamäärällä on raja-arvo
. Siten erotusosamäärällä on raja-arvo
Edellisen lauseen merkitys on siinä, että käänteisfunktion derivaatan määräämiseksi pisteessä 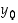 ei tarvitse käänteisfunktion eikä varsinkaan sen derivaatan lauseketta määrätä. Riittää, kun tiedetään minkä pisteen
ei tarvitse käänteisfunktion eikä varsinkaan sen derivaatan lauseketta määrätä. Riittää, kun tiedetään minkä pisteen 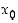 funktio
funktio 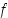 kuvaa kyseiseksi pisteeksi eli milloin
kuvaa kyseiseksi pisteeksi eli milloin 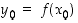 .
.
Opiskelutehtävä 25. (Käänteisfunktion derivaatta)
Määrää funktion 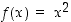 ,
missä
,
missä 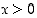 ,
käänteisfunktion derivaatta pisteessä 2 sekä eksplisiittisesti (ratkaisemalla ensin käänteisfunktio), että implisiittisesti (ratkaisematta käänteisfunktiota).
,
käänteisfunktion derivaatta pisteessä 2 sekä eksplisiittisesti (ratkaisemalla ensin käänteisfunktio), että implisiittisesti (ratkaisematta käänteisfunktiota).
Funktio 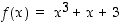 on polynomina derivoituva kaikkialla ja sen derivaatta
on polynomina derivoituva kaikkialla ja sen derivaatta 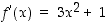 on aina positiivinen. On siis olemassa käänteiskuvaus
on aina positiivinen. On siis olemassa käänteiskuvaus 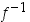 ,
joka on määritelty kuvajoukossa
,
joka on määritelty kuvajoukossa 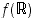 ja on siellä aidosti kasvava. Mikä on kuvajoukko
ja on siellä aidosti kasvava. Mikä on kuvajoukko 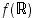 ? Koska
? Koska 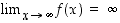 ja
ja 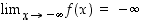 ,
on
,
on 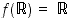 .
.
Määrätään käänteisfunktion derivaatta pisteessä 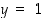 . Edellisen lauseen mukaan se on
. Edellisen lauseen mukaan se on
missä 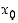 on yhtälön
on yhtälön 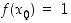 eli yhtälön
eli yhtälön 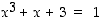 ratkaisu. Kokeilemalla huomataan, että
ratkaisu. Kokeilemalla huomataan, että 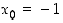 . Bijektiivisyyden takia muita ratkaisuja ei ole, joten kokeilemalla saatu ratkaisu riittää. Siten
. Bijektiivisyyden takia muita ratkaisuja ei ole, joten kokeilemalla saatu ratkaisu riittää. Siten
Edellä olevan mukaan pisteessä 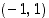 funktion
funktion 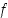 kuvaajan tangentin yhtälö on
kuvaajan tangentin yhtälö on
sekä vastaavasti pisteessä 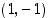 käänteisfunktion
käänteisfunktion 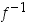 kuvaajan tangentin yhtälö on
kuvaajan tangentin yhtälö on
Tarkastellaan vielä funktion 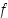 kuvaajan toista pistettä
kuvaajan toista pistettä 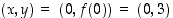 . Sille on
. Sille on
Siten pisteessä 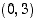 funktion
funktion 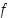 kuvaajan tangentin yhtälö on
kuvaajan tangentin yhtälö on 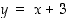 ja vastaavasti pisteessä
ja vastaavasti pisteessä 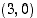 käänteisfunktion
käänteisfunktion 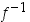 kuvaajan tangentin yhtälö on
kuvaajan tangentin yhtälö on 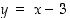 .
.
Näiden tietojen perusteella voisi käänteiskuvausta hahmotella pisteiden 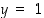 ja
ja 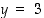 lähistöllä. Funktion ja käänteisfunktion kuvaajat on hahmoteltu graafisen laskimen avulla kuvassa . (Joissakin graafisissa laskimissa käänteiskuvauksen kuvaaja saadaan piirrettyä yksinkertaisesti, kun käytetään ehdon
lähistöllä. Funktion ja käänteisfunktion kuvaajat on hahmoteltu graafisen laskimen avulla kuvassa . (Joissakin graafisissa laskimissa käänteiskuvauksen kuvaaja saadaan piirrettyä yksinkertaisesti, kun käytetään ehdon 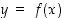 sijasta ehtoa
sijasta ehtoa 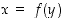 . Tämä edellyttää yleensä, että laskin käsittelee muuttujia
. Tämä edellyttää yleensä, että laskin käsittelee muuttujia 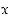 ja
ja 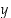 kiinteästi nimettyinä ja että se pystyy piirtämään "peilikuvakuvaajan" eli sellaisen funktion kuvaajan, jossa muuttuja
kiinteästi nimettyinä ja että se pystyy piirtämään "peilikuvakuvaajan" eli sellaisen funktion kuvaajan, jossa muuttuja 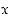 on ilmoitettu muuttujan
on ilmoitettu muuttujan 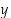 avulla.)
avulla.)
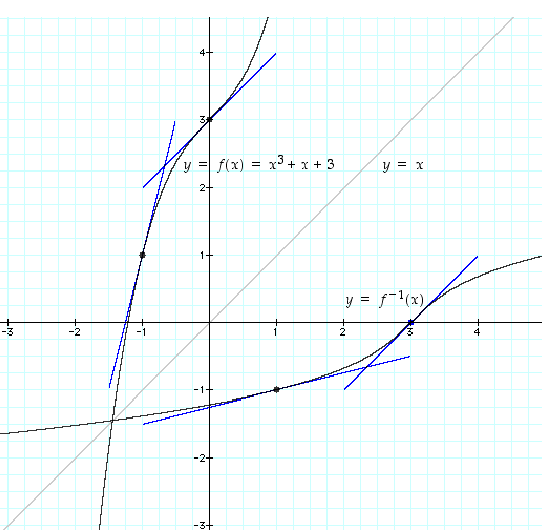
Opiskelutehtävä 26. (Käänteisfunktion kuvaaja)
Ovatko funktiot 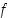 ja
ja 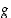 toistensa käänteiskuvauksia, kun niiden kuvaajat ovat:
toistensa käänteiskuvauksia, kun niiden kuvaajat ovat:
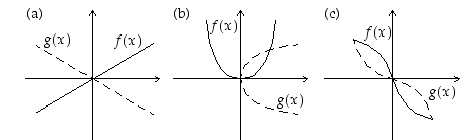
Opiskeluvideo: D10: Käänteisfunktion tangentti 
