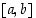 ja derivoituva vastaavalla avoimella välillä
ja derivoituva vastaavalla avoimella välillä 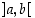 .
.
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Differentiaalilaskennan väliarvolauseen (DVAL) oletuksena on, että funktio on jatkuva suljetulla välillä 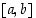 ja derivoituva vastaavalla avoimella välillä
ja derivoituva vastaavalla avoimella välillä 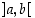 .
.
on muuten selvästi jatkuva kyseisellä suljetulla välillä 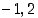 ja derivoituva vastaavalla avoimella välillä
ja derivoituva vastaavalla avoimella välillä 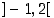 ,
mutta jatkuvuus ja derivoituvuus tulee vielä erikseen tutkia paloittaisen määrittelyn rajakohdassa (
,
mutta jatkuvuus ja derivoituvuus tulee vielä erikseen tutkia paloittaisen määrittelyn rajakohdassa (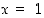 ), sillä se sisältyy tarkasteltavalle välille. Koska
), sillä se sisältyy tarkasteltavalle välille. Koska
Täten 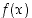 on jatkuva myös kohdassa
on jatkuva myös kohdassa 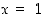 . Lisäksi kohdassa
. Lisäksi kohdassa 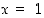 funktion
funktion 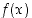 vasemmanpuoleinen derivaatta
vasemmanpuoleinen derivaatta 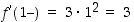 ja oikeanpuoleinen derivaatta
ja oikeanpuoleinen derivaatta 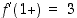 ovat samat (jatkuvuuden takia toispuoleiset derivaatat voidaan määrätä derivaattojen raja-arvoina). Näin ollen
ovat samat (jatkuvuuden takia toispuoleiset derivaatat voidaan määrätä derivaattojen raja-arvoina). Näin ollen 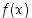 on derivoituva myös kohdassa
on derivoituva myös kohdassa 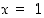 .
.
Täten DVAL:n oletukset toteutuvat ja sen mukaan on olemassa 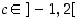 siten, että
siten, että 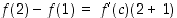 . Kohta
. Kohta 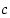 saadaan ratkaistua seuraavasti:
saadaan ratkaistua seuraavasti:
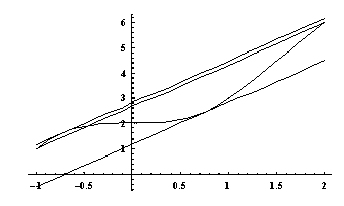
Alla olevassa kuvassa on piirrettynä funktion kuvaaja välillä 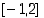 . Kuvan kolmesta suorasta keskimmäinen kulkee pisteiden
. Kuvan kolmesta suorasta keskimmäinen kulkee pisteiden 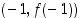 ja
ja 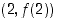 kautta, alin suora vastaa kohdan
kautta, alin suora vastaa kohdan 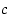 arvoa
arvoa 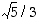 ja ylin suora vastaa kohdan
ja ylin suora vastaa kohdan 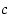 arvoa
arvoa 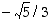 .
.
[Opiskelutehtävä 22] [Vinkki tehtävään 22]