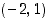 on tehtävässä annetulla käyrällä
on tehtävässä annetulla käyrällä 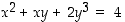 :
:
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Tarkastetaan ensin, onko piste 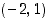 on tehtävässä annetulla käyrällä
on tehtävässä annetulla käyrällä 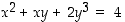 :
:
joten kyseinen piste on käyrällä, koska se toteuttaa annetun yhtälön.
Määritettävän tangentin kulmakerroin on derivaatan arvo pisteessä 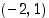 . Derivointi suoritetaan implisiittisesti ja sitä varten käyrän yhtälöön sijoitetaan
. Derivointi suoritetaan implisiittisesti ja sitä varten käyrän yhtälöön sijoitetaan 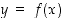 :
:
Derivoidaan yhtälö ja ratkaistaan siitä derivaatta:
Siten tangentin kulmakerroin kohdassa 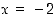 on
on
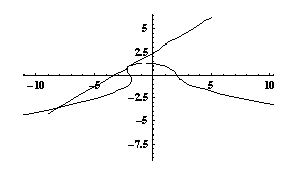
Käyrältä voi etsiä lisää pisteitä ja määrittää niille tangenttisuoria, joiden avulla voi karkeasti hahmotella käyrää. Alla olevassa kuvassa on piirrettynä kyseinen käyrä sekä tehtävässä määritetty tangenttisuora.
[Opiskelutehtävä 21] [Vinkki tehtävään 21]