Implisiittifunktion derivointi
Implisiittiehto 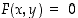 voi määritellä tarkasteltavan pisteen
voi määritellä tarkasteltavan pisteen 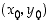 lähistöllä jonkin derivoituvan funktion
lähistöllä jonkin derivoituvan funktion 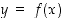 kuvaajan. Sen selvittäminen, milloin näin tapahtuu, kuuluu useamman muuttujan funktioiden teoriaan, ja sivuutetaan siksi tässä. Jos derivoituva ratkaisu
kuvaajan. Sen selvittäminen, milloin näin tapahtuu, kuuluu useamman muuttujan funktioiden teoriaan, ja sivuutetaan siksi tässä. Jos derivoituva ratkaisu 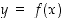 on olemassa, voidaan funktion
on olemassa, voidaan funktion 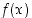 derivaatta tässä pisteessä joskus laskea ratkaisematta itse funktion lauseketta. Seuraavat esimerkit valaisevat tilannetta.
derivaatta tässä pisteessä joskus laskea ratkaisematta itse funktion lauseketta. Seuraavat esimerkit valaisevat tilannetta.
Esimerkki 3.4.6.
Tarkastellaan esimerkin 3.4.4 yhtälöä  jonkin pisteen lähistöllä. Kun yhtälöön sijoitetaan esimerkiksi
jonkin pisteen lähistöllä. Kun yhtälöön sijoitetaan esimerkiksi 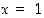 ,
nähdään, että
,
nähdään, että 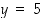 . Tarkastellaankin yhtälöä pisteen
. Tarkastellaankin yhtälöä pisteen 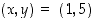 lähistöllä. Oletetaan nyt (tietämättä eksplisiittistä ratkaisua!), että tarkasteltava yhtälö määrittelee jollain pisteen
lähistöllä. Oletetaan nyt (tietämättä eksplisiittistä ratkaisua!), että tarkasteltava yhtälö määrittelee jollain pisteen 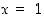 sisältävällä välillä derivoituvan funktion
sisältävällä välillä derivoituvan funktion 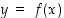 . (Esimerkin 3.4.4 eksplisiittisestä ratkaisusta näkee, että näin todella onkin.) Silloin yhtälö toteutuu, kun siihen sijoitetaan
. (Esimerkin 3.4.4 eksplisiittisestä ratkaisusta näkee, että näin todella onkin.) Silloin yhtälö toteutuu, kun siihen sijoitetaan 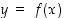 ,
eli kun
,
eli kun
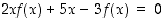 .
.
Derivoimalla tämän yhtälön eri puolet erikseen saadaan yhtälö
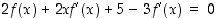 .
.
Huomaa, että lauseke 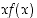 piti derivoida tulon derivoimissäännöllä:
piti derivoida tulon derivoimissäännöllä: 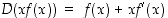 . Sijoittamalla saatuun yhtälöön
. Sijoittamalla saatuun yhtälöön 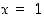 saadaan yhtälö
saadaan yhtälö
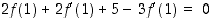 ,
,
mistä ehto 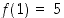 huomioiden saadaan yhtälö
huomioiden saadaan yhtälö
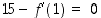 .
.
Tästä nähdään, että 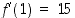 . Sen lisäksi, että mahdollinen ratkaisukäyrä kulkee pisteen
. Sen lisäksi, että mahdollinen ratkaisukäyrä kulkee pisteen 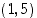 kautta, tiedämme nyt myös, että siinä pisteessä ratkaisukäyrän tangentin kulmakerroin on 15. On huomattava, että tämän tiedon selvittämiseen ei edellä ole tarvittu eksplisiittistä ratkaisua.
kautta, tiedämme nyt myös, että siinä pisteessä ratkaisukäyrän tangentin kulmakerroin on 15. On huomattava, että tämän tiedon selvittämiseen ei edellä ole tarvittu eksplisiittistä ratkaisua.
Vertaillaan vielä tulosta esimerkistä 3.4.4 suoraan saatavaan tulokseen. Edellä olevan ratkaisuketjun kolmanneksi viimeisestä yhtälöstä voidaan nimittäin yleisesti ratkaista derivaatan lausekkeeksi
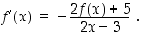
Kun siihen sijoitetaan esimerkissä 3.4.4 ratkaistu funktion lauseke
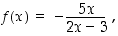
saadaan derivaatalle lauseke
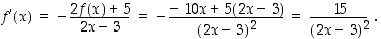
Sama tulos saadaan tietenkin derivoimalla suoraan funktion lauseke. Joka tapauksessa tämänkin mukaan 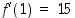 .
.

Edellisessä esimerkissä tehtyä menettelyä, jossa funktion implisiittisesti määrittelevä yhtälö derivoidaan ennen funktion tai sen derivaatan ratkaisemista, sanotaan implisiittiseksi derivoinniksi. Menettelyn etuna on se, että funktion lauseketta ei tarvitse (varsinkaan jos sitä ei voi) ratkaista ja silti ratkaisufunktion derivaatta pystytään usein selvittämään. Derivaatan ja sitä myötä tangentin avulla pystytään edelleen arvioimaan ratkaisukäyrän kulkua tarkastelupisteen lähistöllä.
Esimerkki 3.4.7.
Määrätään yhtälön 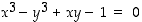 määräämän funktion
määräämän funktion 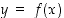 kuvaajan tangentti pisteessä
kuvaajan tangentti pisteessä 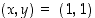 . Huomaa, että muuttujaa
. Huomaa, että muuttujaa 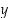 olisi vaikea eksplisiittisesti ratkaista annetusta yhtälöstä.
olisi vaikea eksplisiittisesti ratkaista annetusta yhtälöstä.
Ensinnäkin todetaan, että piste 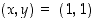 toteuttaa annetun yhtälön:
toteuttaa annetun yhtälön: 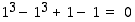 . Oletetaan sitten, että derivoituva funktio
. Oletetaan sitten, että derivoituva funktio 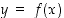 toteuttaa annetun yhtälön, jolloin siis
toteuttaa annetun yhtälön, jolloin siis
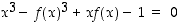 .
.
Derivoidaan yhtälö implisiittisesti, jolloin saadaan yhtälö
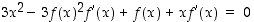 .
.
Sijoitetaan yhtälöön arvot 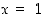 ja
ja 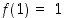 :
:
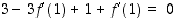 .
.
Tästä saadaan ratkaisuksi 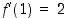 . Kysytyn tangentin yhtälö on siten
. Kysytyn tangentin yhtälö on siten
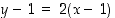 eli
eli 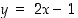 .
.
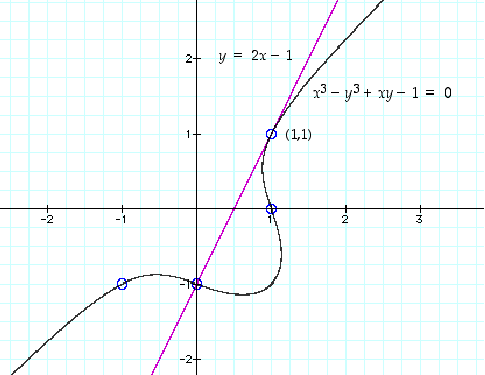
Kuvaan 36 on hahmoteltu annetun yhtälön toteuttava ratkaisukäyrä ja edellä laskettu tangentti. Huomaa, että käyrä ei voi selvästikään olla yhden funktion kuvaaja.
Kuva 36.
Annettua yhtälöä 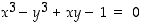 edelleen tutkimalla voi huomata, että myös pisteet
edelleen tutkimalla voi huomata, että myös pisteet 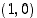 ,
,
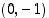 ja
ja 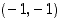 toteuttavat sen. Toistamalla edellä olevat tarkastelut näiden pisteiden suhteen saadaan näitten pisteitten kautta kulkevat tangentit selville. Tuloksia voi verrata kuvan 36 hahmotelmaan.
toteuttavat sen. Toistamalla edellä olevat tarkastelut näiden pisteiden suhteen saadaan näitten pisteitten kautta kulkevat tangentit selville. Tuloksia voi verrata kuvan 36 hahmotelmaan.

Opiskelutehtävä 21. (Implisiittisen funktion derivaatta)
Määrää yhtälön 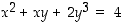 toteuttavan käyrän
toteuttavan käyrän 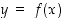 tangentti pisteessä
tangentti pisteessä 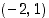 . (Etsi käyrältä muita pisteitä ja hahmottele käyrää.)
. (Etsi käyrältä muita pisteitä ja hahmottele käyrää.)
Vinkki tehtävään 21
Opiskeluvideo: D6: Implisiittinen derivointi 

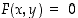 voi määritellä tarkasteltavan pisteen
voi määritellä tarkasteltavan pisteen 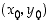 lähistöllä jonkin derivoituvan funktion
lähistöllä jonkin derivoituvan funktion 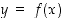 kuvaajan. Sen selvittäminen, milloin näin tapahtuu, kuuluu useamman muuttujan funktioiden teoriaan, ja sivuutetaan siksi tässä. Jos derivoituva ratkaisu
kuvaajan. Sen selvittäminen, milloin näin tapahtuu, kuuluu useamman muuttujan funktioiden teoriaan, ja sivuutetaan siksi tässä. Jos derivoituva ratkaisu 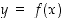 on olemassa, voidaan funktion
on olemassa, voidaan funktion 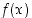 derivaatta tässä pisteessä joskus laskea ratkaisematta itse funktion lauseketta. Seuraavat esimerkit valaisevat tilannetta.
derivaatta tässä pisteessä joskus laskea ratkaisematta itse funktion lauseketta. Seuraavat esimerkit valaisevat tilannetta.  jonkin pisteen lähistöllä. Kun yhtälöön sijoitetaan esimerkiksi
jonkin pisteen lähistöllä. Kun yhtälöön sijoitetaan esimerkiksi 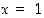 ,
nähdään, että
,
nähdään, että 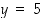 . Tarkastellaankin yhtälöä pisteen
. Tarkastellaankin yhtälöä pisteen 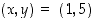 lähistöllä. Oletetaan nyt (tietämättä eksplisiittistä ratkaisua!), että tarkasteltava yhtälö määrittelee jollain pisteen
lähistöllä. Oletetaan nyt (tietämättä eksplisiittistä ratkaisua!), että tarkasteltava yhtälö määrittelee jollain pisteen 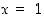 sisältävällä välillä derivoituvan funktion
sisältävällä välillä derivoituvan funktion 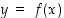 . (Esimerkin
. (Esimerkin 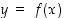 ,
eli kun
,
eli kun 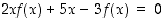 .
. 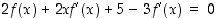 .
. 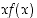 piti derivoida tulon derivoimissäännöllä:
piti derivoida tulon derivoimissäännöllä: 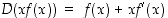 . Sijoittamalla saatuun yhtälöön
. Sijoittamalla saatuun yhtälöön 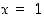 saadaan yhtälö
saadaan yhtälö 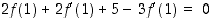 ,
,
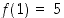 huomioiden saadaan yhtälö
huomioiden saadaan yhtälö 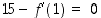 .
. 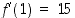 . Sen lisäksi, että mahdollinen ratkaisukäyrä kulkee pisteen
. Sen lisäksi, että mahdollinen ratkaisukäyrä kulkee pisteen 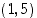 kautta, tiedämme nyt myös, että siinä pisteessä ratkaisukäyrän tangentin kulmakerroin on 15. On huomattava, että tämän tiedon selvittämiseen ei edellä ole tarvittu eksplisiittistä ratkaisua.
kautta, tiedämme nyt myös, että siinä pisteessä ratkaisukäyrän tangentin kulmakerroin on 15. On huomattava, että tämän tiedon selvittämiseen ei edellä ole tarvittu eksplisiittistä ratkaisua. 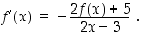
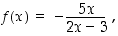
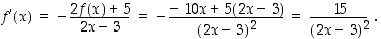
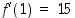 .
. 
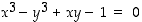 määräämän funktion
määräämän funktion 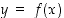 kuvaajan tangentti pisteessä
kuvaajan tangentti pisteessä 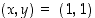 . Huomaa, että muuttujaa
. Huomaa, että muuttujaa 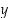 olisi vaikea eksplisiittisesti ratkaista annetusta yhtälöstä.
olisi vaikea eksplisiittisesti ratkaista annetusta yhtälöstä. 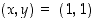 toteuttaa annetun yhtälön:
toteuttaa annetun yhtälön: 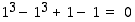 . Oletetaan sitten, että derivoituva funktio
. Oletetaan sitten, että derivoituva funktio 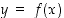 toteuttaa annetun yhtälön, jolloin siis
toteuttaa annetun yhtälön, jolloin siis 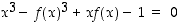 .
. 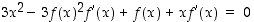 .
. 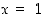 ja
ja 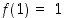 :
: 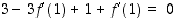 .
. 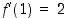 . Kysytyn tangentin yhtälö on siten
. Kysytyn tangentin yhtälö on siten 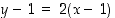 eli
eli 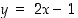 .
. 
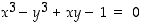 edelleen tutkimalla voi huomata, että myös pisteet
edelleen tutkimalla voi huomata, että myös pisteet 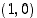 ,
,
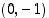 ja
ja 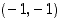 toteuttavat sen. Toistamalla edellä olevat tarkastelut näiden pisteiden suhteen saadaan näitten pisteitten kautta kulkevat tangentit selville. Tuloksia voi verrata kuvan
toteuttavat sen. Toistamalla edellä olevat tarkastelut näiden pisteiden suhteen saadaan näitten pisteitten kautta kulkevat tangentit selville. Tuloksia voi verrata kuvan 
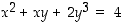 toteuttavan käyrän
toteuttavan käyrän 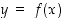 tangentti pisteessä
tangentti pisteessä 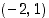 . (Etsi käyrältä muita pisteitä ja hahmottele käyrää.)
. (Etsi käyrältä muita pisteitä ja hahmottele käyrää.) 
