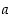 ja
ja 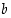 ,
joille
,
joille 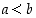 ,
on olemassa sellainen rationaaliluku
,
on olemassa sellainen rationaaliluku 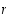 ,
että
,
että 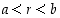 ja myös sellainen irrationaaliluku
ja myös sellainen irrationaaliluku 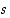 ,
että
,
että 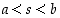 .
.
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Tarkastelemme nyt sitä, kuinka paljon rationaali- ja reaalilukuja toisiinsa verrattuna on olemassa. Seuraava tulos osoittaa, että kahden reaaliluvun välissä on aina sekä rationaali- että irrationaalilukuja.
Kaikille reaaliluvuille 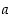 ja
ja 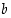 ,
joille
,
joille 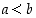 ,
on olemassa sellainen rationaaliluku
,
on olemassa sellainen rationaaliluku 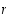 ,
että
,
että 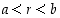 ja myös sellainen irrationaaliluku
ja myös sellainen irrationaaliluku 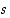 ,
että
,
että 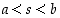 .
.
Todistus. Osoitetaan ensin väitetynlaisen rationaaliluvun olemassaolo. Koska 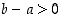 ,
on Arkhimedeen lain mukaan olemassa kokonaisluku
,
on Arkhimedeen lain mukaan olemassa kokonaisluku 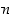 ,
jolle
,
jolle 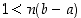 . Valitaan edelleen kokonaisluku
. Valitaan edelleen kokonaisluku 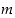 ,
jolle
,
jolle 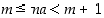 . Silloin
. Silloin
mistä valinnalla 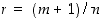 saadaan haluttu tilanne
saadaan haluttu tilanne 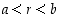 .
.
Lauseen toinen väite eli irrationaaliluvun olemassaolo kahden reaaliluvun välissä jätetään harjoitustehtäväksi (tehtävä 25).
Edellinen lause osoittaa siis, että kahden reaaliluvun välissä on aina rationaalilukuja. Sanotaankin, että rationaalilukuja on tiheästi reaalilukujen joukossa. Tämä mahdollistaa sen käytännön laskennan kannalta tärkeän tosiasian, että jokaista reaalilukua voidaan approksimoida rationaaliluvuilla mielivaltaisen tarkasti. Toisaalta tämä tiheystulos ei kuitenkaan ilmoita vielä mitään näiden lukujen paljoudesta. Osoittautuu, että lukumäärämielessä (tarkemmin puhutaan joukkojen mahtavuudesta) irrationaalilukuja on kuitenkin paljon enemmän kuin rationaalilukuja. Rationaaliluvut voidaan nimittäin periaatteessa numeroida eli niitä on yhtä paljon kuin luonnollisia lukuja, mutta irrationaaliluvuille vastaavaa numerointia ei voida tehdä. Näitten tulosten perustelu sivuutetaan tässä.